Högskoleprovet matte
XYZ, KVA, NOG OCH DTK
En del bävar inför högskoleprovets matematiska delar. Frågorna verkar så krångliga och man är inte säker på exakt hur man förväntas räkna för att komma fram till svaret. Nedan hittar du allt du behöver veta om högskoleprovets kvantitativa delar – XYZ, KVA, NOG, DTK. Med Allakandos onlinekurs får du allt som behövs, prova gratis nu!
306 omdömen

Matte högskoleprovet – Vad ingår i de kvantitativa provpassen på högskoleprovet?
Kvantitativa uppgifter utgör hälften av högskoleprovets 160 poäng. Varje kvantitativt provpass består av 40 uppgifter fördelat på fyra olika delprov – XYZ, KVA, NOG, och DTK. De olika delarna med högskoleprovet matte innehåller både uppgifter som testar din förståelse för olika matematiska koncept, men också uppgifter som testar mer generellt logiskt tänkande och analytisk problemlösning. Varje provpass är 55 minuter långt, men uppgifterna på högskoleprovet matte tar olika lång tid även om de alla är värda lika många poäng.
De 40 uppgifterna i ett provpass i matematik på högskoleprovet är uppdelade på följande vis:
- Högskoleprovet matte: XYZ – 12 uppgifter
- Högskoleprovet matte: KVA – 10 uppgifter
- Högskoleprovet matte: NOG – 6 uppgifter
- Högskoleprovet matte: DTK – 12 uppgifter
Här går vi kort igenom de olika delproven som finns på högskoleprovet matte med exempel på den typ av uppgifter du kan komma att se på provet. Uppgifterna är tagna från gamla högskoleprov, men förklaringarna är från vårt onlineverktyg.
XYZ – Matematisk problemlösning
XYZ testar matematisk problemlösning. Delprovet i matte består av 12 uppgifter, och den rekommenderade provtiden är 12 minuter, så du har 1 minut på dig per uppgift. Områdena som testas på XYZ är aritmetik, algebra, geometri, funktioner, och statistik.
EXEMPELUPPGIFT HÖGSKOLEPROVET MATTE
Uppgiftsformulering:
Vad är (\sqrt5 \over 5) ?
Alternativ:
- (1\over 5)
- (1)
- (\sqrt5)
- (3)
Förklaring:
Vi kan lösa den här uppgiften på ett par olika sätt – antingen genom att göra om bråket till potenser, eller genom ett lite finurligare sätt.
Vi börjar med att göra om bråket till potenser, då de ofta är enklare att arbeta med. Vi vet att ta roten ur ett tal är samma sak som att ta talet upphöjt till (\frac{1}{2}). Alltså har vi att [\frac{\sqrt 5}{3} = \frac{5^\frac{1}{2}}{5}]
Vi vet också att alla tal kan skrivas som sig själva upphöjt till 1. Vi kan alltså skriva om bråket ytterligare så att vi får: [\frac{5^\frac{1}{2}}{5} = \frac{5^\frac{1}{2}}{5^1}]
Nu kan vi använda de vanliga potenslagarna för att få: [\frac{5^\frac{1}{2}}{5^1} = 5^{-\frac{1}{2}}] Ett tal upphöjt till ett negativt tal är samma sak som 1 delat med talet upphöjt till samma tal fast positivt. Alltså får vi slutligen att: [5^{-\frac{1}{2}} = \frac{1}{5^\frac{1}{2}} = \frac{1}{\sqrt 5}] Rätt svar är alltså A.
Vi hade också kunnat lösa uppgiften genom att direkt från början notera att vi kan skriva 5 som (\sqrt 5 \cdot \sqrt 5). Vi får då: [\frac{\sqrt 5}{5} = \frac{\sqrt 5}{\sqrt 5 \cdot \sqrt 5}] Vi förkortar med (\sqrt 5) uppe och nere och får då slutligen: [\frac{\sqrt 5}{\sqrt 5 \cdot \sqrt 5} = \frac{1}{\sqrt 5}]Rätt svar är alltså A.
KVA – Kvantitativa jämförelser
KVA testar kvantitativa jämförelser. Delprovet består av 10 uppgifter, och den rekommenderade provtiden är 10 minuter, så du har 1 minut på dig per uppgift.
Uppgifterna på KVA består av en beskrivning av två kvantiteter, kvantitet I och kvantitet II. Din uppgift är att bestämma vilken av de båda kvantiteterna som är störst med hjälp av den information som ges i uppgiften. Svarsalternativen är alltid desamma oavsett uppgiften: ,
- I är större än II
- II är större än I
- I är lika med II
- Informationen är otillräcklig
Uppgift:
Kvantitet I:({1\over 5} + {1 \over 5} )
Kvantitet II:({1\over 4} + {3 \over 20} )
Alternativ:
- I är större än II
- II är större än I
- I är lika med II
- Informationen är otillräcklig
Förklaring:
Det är svårt att jämföra bråk som inte har samma nämnare (talet där nere). För att enklare kunna jämföra kvantiteterna vill vi först skriva om dem så att de har samma nämnare. Den största nämnaren är 20, vilket är delbart med både 4 och 5. Vi kan alltså göra om de andra bråken till tjugodelar och sedan jämföra!
Kvantitet I: Vi gör om de här bråken till tjugodelar genom att multiplicera med 4 både uppe och nere så att vi får 20 i nämnaren:\frac{1 \color{red}{\cdot 4}}{5\color{red}{\cdot 4}} + \frac{1\color{red}{\cdot 4}}{5\color{red}{\cdot 4}} = \frac{4}{20} + \frac{4}{20} = \frac{4 + 4}{20} = \frac{8}{20}
Kvantitet II: På samma sätt gör vi om \frac{1}{4} till tjugodelar genom att multiplicera med 5 uppe och nere så att vi får 20 i nämnaren: \frac{1\color{red}{\cdot 5}}{4\color{red}{\cdot 5}} + \frac{3}{20} = \frac{5}{20} + \frac{3}{20} = \frac{5+3}{20} = \frac{8}{20}
De två kvantiteterna är alltså lika stora, och rätt svar är därmed C.
NOG – Kvantitativa resonemang
NOG testar kvantitativa resonemang. Delprovet består av 6 uppgifter där du ska avgöra om det finns nog med information för att besvara lösa uppgiften. Rekommenderad tid för delprovet är 10 minuter, så du har alltså 1.5 minut på dig per uppgift.
I varje uppgift får du inledande information och en fråga, markerad i fet stil. Därefter får du ytterligare information i form av två påståenden, påstående 1 och påstående 2. Uppgiften är då att avgöra om den information som ges i påstående 1 och 2 räcker för att besvara frågan entydigt . Uppgifterna på NOG börjar alltid med ”Tillräcklig information för att lösa uppgiften erhålls”, och har alltid samma fem svarsalternativ för att avsluta den meningen:
- i (1) men ej i (2)
- i (2) men ej i (1)
- i (1) tillsammans med (2)
- i (1) och (2) var för sig
- ej genom de båda påståendena
Alternativen tolkas som följande:
- Vi kan lösa uppgiften med enbart informationen i (1). Vi kan inte lösa uppgiften med enbart informationen i (2).
- Vi kan lösa uppgiften med enbart informationen i (2). Vi kan inte lösa uppgiften med enbart informationen i (1).
- Vi kan lösa uppgiften med informationen i (1) och (2) tillsammans, men inte med enbart (1) eller (2).
- Vi kan lösa uppgiften med enbart informationen i (1). Vi kan också lösa uppgiften med enbart informationen i (2).
- Vi kan inte lösa uppgiften ens med informationen från både (1) och (2) tillsammans.
Uppgift:
På en bondgård finns 63 djur: hästar, kor och grisar. Hur många kor finns det på bondgården?
Alternativ:
- i (1) men ej i (2)
- i (2) men ej i (1)
- i (1) tillsammans med (2)
- i (1) och (2) var för sig
- ej genom de båda påståendena
Förklaring:
Vi benämner antalet hästar, kor, och grisar h, k, och g. Det finns 72 djur på bondgården totalt, så vi vet att h + k + g = 73. Vi vill veta hur många kor det finns på bondgården, alltså vad k är.
Information från (1)
Antalet grisar g är dubbelt så stort som antalet hästar h och kor k tillsammans. Det kan vi skriva som g = 2(h+k). Tillsammans med ekvationen från uppgiften så har vi då:
h + k + g = 72
g = 2(h+k)
Vi har alltså två ekvationer med tre obekanta. Eftersom vi har fler ekvationer än obekanta kan vi inte lösa uppgiften.
Information från (2)
Antalet hästar h på bondgården är hälften av antalet kor k. Det kan vi skriva som h =(\frac{k}{2}). Tillsammans med ekvationen från uppgiften så har vi då:
h + k + g = 72
h = (\frac{k}{2})
Vi har alltså två ekvationer med tre obekanta. Eftersom vi har fler ekvationer än obekanta kan vi inte lösa uppgiften.
Information från (1) och (2)
Från informationen i (1) kunde vi skriva ekvationen g = 2(h+k). Från information i (2) kunde vi skriva ekvationen h = (\frac{k}{2}). Tillsammans med ekvationen från uppgiften ger det oss:
h + k + g = 72
g = 2(h+k)
h = (\frac{k}{2})
Vi har alltså tre oberoende ekvationer med tre obekanta. Eftersom vi har lika många oberoende ekvationer som obekanta så kan vi lösa uppgiften!
Slutsats
Vi behövde informationen från (1) och (2) tillsammans för att kunna lösa uppgiften.
Rätt svar är därmed C.
DTK – Diagram, tabeller, och kartor
DTK består av olika sorters diagram, tabeller, och kartor. Delprovet består av 12 uppgifter där du ska utläsa och tolka informationen som ges i figurerna. Rekommenderar provtid för DTK är 23 minuter, vilket innebär att du har ungefär 115 sekunder per uppgift. Varje uppgift har fyra alternativ, och du ska välja det som bäst besvarar frågan, vilket innebär att svaren ibland är ungefärliga.
EXEMPELUPPGIFT HÖGSKOLEPROVET MATTE
Uppgift:
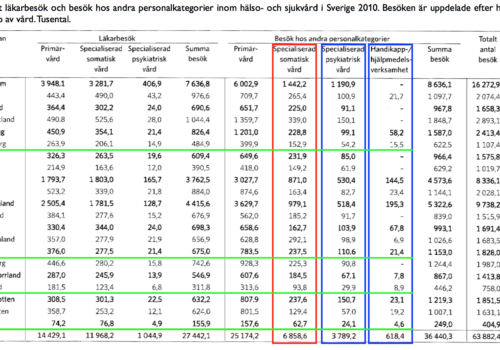
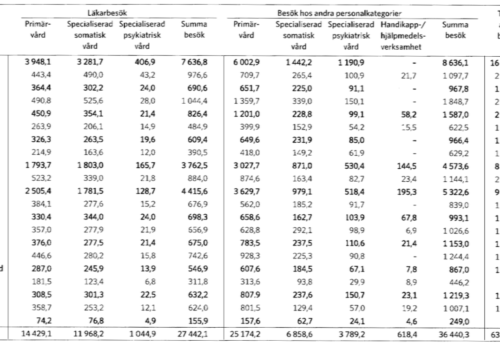
Vilken huvudman avses? Antalet besök hos andra personalkategorier var inom specialiserad somatisk vård mindre än 100 000 och inom specialiserad somatisk vård mer än tio gånger så stort som inom handikapp/hjälpmedelsverksamhet.
Alternativ:
- Kronoberg
- Dalarna
- Jämtland
- Gotland
Förklaring:
Vi vill veta vilken av huvudmännen som stämmer överens med båda påståenden. Det smidigaste sättet att lösa den här typen av uppgifter är att först hitta de delar av tabellen som påståendena avser. Det första påståendet avser specialiserad somatisk vård, så vi markerar den kolumnen med rött. Det andra påståendet avser specialiserad psykiatrisk vård och handikapp-/hjälpmedelsverksamhet, så vi markerar de kolumnerna med blått. Vi markerar sedan de fyra huvudmännen med grönt.
Vi börjar med det första påståendet – ”antalet besök hos andra specialkategorier inom specialiserad somatisk vård var mindre än 100 000”. De enda huvudmän som har mindre än 100 i den kolumnen är Jämtland och Gotland, så vi kan utesluta alternativ A och B.
Vi fortsätter med det andra påståendet – ”antalet besök inom specialiserad psykiatrisk vård var fem gånger så stort som inom handikapp-/hjälpmedelsverksamhet”. I Jämtland så var antalet besök inom specialiserad somatisk vård 93.8 och inom handikapp-/hjälpmedelsverksamhet 8.9. Vi ser då att 8.9 x 10 = 89 < 93.8, så antalet besök inom specialiserad somatisk vård var alltså mer än 10 gånger så mycket som antalet besökt inom handikapp-/hjälpmedelsverksamhet.
Vi har hittat en huvudman som stämmer med båda påståenden, så vi behöver inte undersöka Gotland. Rätt svar är därmed C.
Mer information om högskoleprovet matte
I vårt onlineverktyg så går vi igenom alla provdelar i detalj, inte minst om matte högskoleprovet. Du får utförliga genomgångar av materialet på provet, förklaringar till tusentals uppgifter, och lär dig expertframtagna strategier och knep för att klara allt som kan tänkas komma på provet.
Tillbaka till startsidan: Högskoleprovet
Även om du aldrig har varit så bra på matematiskt tänkande så ska du veta att även du kan förstå högskoleprovet matte! Med vår kurs så blir upplägget glasklart. Du får pedagogiska förklaringar som gör det möjligt för dig att få en högre poäng på dessa delar och på det samlade provet.
Lär dig matte för högskoleprovet
Om det är så att du har glömt bort de formler som kommer att bli nödvändiga då man skriver högskoleprovdet så ska du veta att du får dessa av vår onlinekurs. Vi har till och med skapat videos som visar dig den matte högskoleprovet kräver. Det här gör det så mycket enklare att förstå och att klara frågorna. Sitt med vår kurs i lugn och ro, och ta dig igenom de bitar som känns lite svåra. Det kommer inte att ta lång tid innan du upplever att du faktiskt börjar få bra koll just på matematiken!
Måste man ha högsta betyg i matte för högskoleprovet?
Nej, man måste inte ha högsta betyg på gymnasiets alla kurser för att klara högskoleprov matte. Högskoleprovet matte-del kräver egentligen bara grundläggande kunskaper. Om det är något som du har missat så kommer du snabbt att ta igen detta med vår onlinekurs. Det rör sig verkligen inte om något omöjligt. Du kan alltså få 2.0 på nästa prov utan att ha högsta betyg i skolan. Det gäller att träna rätt inför högskoleprovet matte.
Vikten av att lära sig strukturen på frågorna inom matematik
När du pluggar matte inför högskoleprovet med vår onlinekurs så är det inte bara formlerna som du lär in. Du kommer också att se strukturen och snabbt koppla ihop varje del med den matematik på högskoleprovet som faktiskt krävs. Det är på så vis som du kan plugga matte inför högskoleprovet på ett fokuserat sätt som ger resultat.
Genom att ge dig gamla högskoleprov med matte & matematik så övar du på precis samma typ av frågor som kommer att dyka upp vid nästa provtillfälle. Det blir nya nummer och andra svar, men allt annat är detsamma så du kommer att känna igen dig vilket är viktigt då du vill tänka rätt från start.
Utvecklas snabbt och effektivt på högskoleprovets matte
Det kan kännas lite motigt att jobba med den matte högskoleprovet kräver då man inte är intresserad av detta ämne. Men med vår kurs så blir det ändring på detta. Då du får pedagogiska förklaringar för att öva på högskoleprovet matte med filmer och en coach att prata med. Då blir det rentav ett nöje att plugga just på matten. Du kommer att se hur du utvecklas och det kan kännas som en seger att äntligen få rätt på frågorna som tidigare såg helt omöjliga ut. Vi visar dig hur du ska räkna, använda strategi och på andra sätt klara matte till högskoleprovet.
När du är klar med vår onlinekurs så är du redo att möta verkliga högskoleprovet matte exempel, och du ska inte bli förvånad om du lyckas få alla rätt på mattedelarna. Har du förberett dig väl så kommer du att ha chansen att få en riktigt hög poäng på provet, även på mattedelarna. Det kan vara detta som ger dig inträdesbiljetten till den högskoleutbildning som du siktar mot. Prova dig själv med unika test för matematiken.
Tre alternativ: Så lär vi dig all matte inför högskoleprovet

Webbkurs med garanterad höjning
Plugga smart på uppgifter med förklaringar. Här finns all matte på högskoleprovet tillgängligt, med en fullständig videoguide.

Intensivkurs: Lär dig allt på 2 dagar
Under två effektiva dagar inför högskoleprovet går vårt expert-team igenom allt du behöver kunna för att nå toppresultat!

Skräddarsydd HP-coachning
Få en personlig expertcoach som ger dig skräddarsydda lektioner. Fokusera på precis det du behöver för att nå ditt mål på högskoleprovet!