Vektor
När man vill beskriva storleken av en kvantitet så kan man använda vanliga tal. Men hur gör man om man vill beskriva inte bara storlek utan även riktningen hos ett fenomen? Då kan man använda vektorer! Som exempel så kanske man färdas 70 km/h österut. Då är 70 km/h storleken och öster är riktningen. Med andra ord är hastigheten en vektor med storleken 70 km/h och riktningen öster.
För att behandla vektorer visuellt så ritar man ofta pilar i ett koordinatsystem, eftersom pilar kan ha både storlek (längden på pilen) och riktning. Utifrån koordinatsystemet kan man då ange vektorns koordinater, som beräknas som skillnaden mellan koordinaterna för pilens startpunkt och pilens slutpunkt.
Räkneexempel och förklaringar
Exempel: Vad för koordinater har vektorerna i bilden?
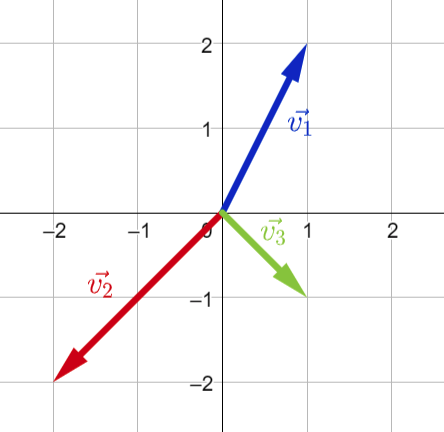
Vi börjar med \vec{v_1}, vars ändpunkt har x-koordinaten 1 och y koordinaten 2. Startpunkten är i origo, med x-koordinat 0 och y-koordinat 0. Därför har vektorn en x-koordinat som är 1 - 0 = 1 och en y-koordinat som är 2 - 0 = 2. Alltså är vektorns koordinater (2, 1).
Notera att när startpunkten är i origo så kommer vektorns koordinater vara samma sak som ändpunktens koordinater, eftersom vi bara kommer ta minus 0 ner vi tar ändpunkten minus startpunkten.
Om vi nu kollar på \vec{v_2} så ser vi att igen så ligger startpunkten i origo, så igen kommer vektorns koordinater vara samma som ändpunktens koordinater. Vi ser att x-koordinaten för vektorns ändpunkt är -2 och y-koordinaten är -2, så vektorns koordinater är (-2, -2).
Slutligen har vi \vec{v_3}, som också har startpunkt i origo. Ändpunkten har x-koordinaten 1 och y-koordinaten -1, så vektorns koordinater är (1, -1).
Exempel: Vad för koordinater har vektorerna i bilden?
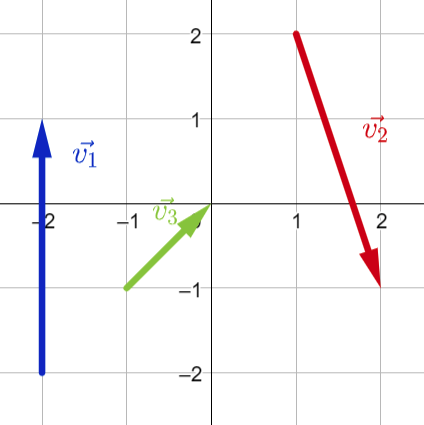
Vi kan igen börja med \vec{v_1}. Där har startpunkten x-koordinaten -2, och ändpunkten har x-koordinaten -2. Alltså är vektorns x-koordinat (-2) - (-2) = 0.
Sedan så har startpunkten y-koordinaten -2 och ändpunkten har y-koordinaten 1, så vektorns y-koordinat blir 1 - (-2) = 3.
Alltså är vektorns koordinater \vec{v_1} = (0,3).
Om vi nu kollar på \vec{v_2} så ser vi att startpunktens koordinater är (1, 2) medan ändpunkten har koordinaterna (2, -1). Därför blir vektorns x-koordinat 2 - 1 = 1 och dess y-koordinat blir (-1) - 2 = -3.
Alltså är vektorns koordinater \vec{v_2} = (1,-3).
Slutligen kollar vi på \vec{v_3}, vars startpunkt har koordinaterna (-1, -1) och ändpunkt har koordinaterna (0, 0). Alltså är vektorns x-koordinat 0 - (-1) = 1 och vektorns y-koordinat är 0 - (-1) = 1.
Så vektorn har koordinater (1,1).
Övningsuppgifter
Frågor med svarsalternativ:
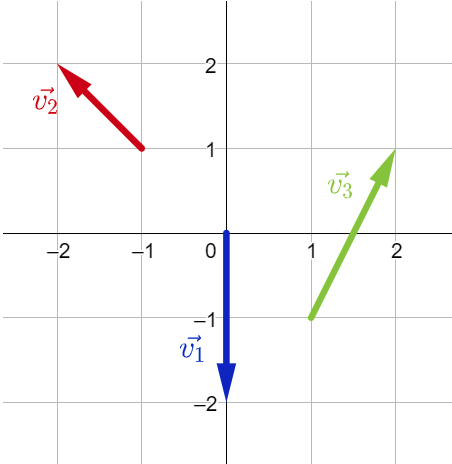
Fråga 1: Vad har vektorn \vec{v_1} för koordinater?
Svarsalternativ 1.1: (2,0)
Svarsalternativ 1.2: (0,2)
Svarsalternativ 1.3: (-2,0)
Svarsalternativ 1.4: (0,-2) (rätt)
Fråga 2: Vad har vektorn \vec{v_2} för koordinater?
Svarsalternativ 2.1: (-1,1) (rätt)
Svarsalternativ 2.2: (-2,2)
Svarsalternativ 2.3: (1,-1)
Svarsalternativ 2.4: (2,-2)
Fråga 3: Vad har vektorn \vec{v_3} för koordinater?
Svarsalternativ 3.1: (2,1)
Svarsalternativ 3.2: (1,2) (rätt)
Svarsalternativ 3.3: (1,1)
Svarsalternativ 3.4: (2,2)
Så hjälper Allakando dig till toppresultat i skolan
Mattehjälp för alla åldrar
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.
Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!
Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!
