Trigonometri
Inom trigonometrin finns tre olika funktioner som beskriver sambandet mellan sidorna och vinklarna i en rätvinklig triangel. Funktionerna kallas för sinus, cosinus och tangens. Vi förkortar de som sin, cos och tan. Vi kallar dessa funktioner för trigonometriska funktioner. I den här guiden går vi igenom hur de fungerar och används!
Trigonometri – sin, cos och tan
Formler för trigonometriska funktioner:
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}
cos\;v=\frac{n\"arliggande\;katet}{hypotenusa}
tan\;v=\frac{motst{\aa}ende\;katet}{n\"arliggande\;katet}
För varje vinkel, v, finns alltså ett visst värde för sinus, cosinus och tangens. Sin, cos och tan är alltså inte ett tal som vi multiplicerar med vinkeln, v, utan en benämning på en funktion. Värdet för funktionerna vid en viss vinkel får vi via vår miniräknare, som har funktionerna inprogrammerade.
Om vi har värdet på en av triangelns sidor och en av triangelns vinklar (förutom den räta vinkeln), så kan vi ta reda på värdet av en av de obekanta sidorna med hjälp av sinus, cosinus eller tangens. Vi ser ett exempel på detta nedan.
Vad är trigonometri?
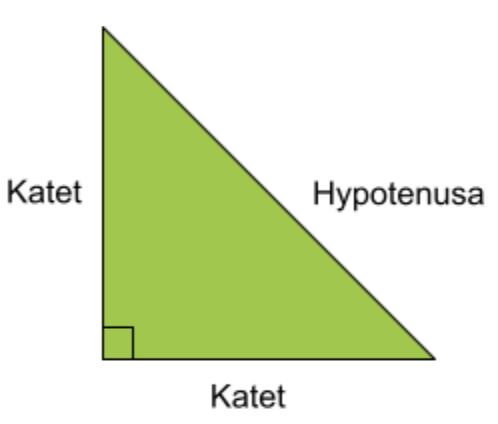
Trigonometri beskriver sambandet mellan sidor och vinklar i rätvinkliga trianglar. En rätvinklig triangel är en triangel som innehåller en rät, 90-gradig vinkel. Den räta vinkeln markeras med en liten kvadrat i hörnet (□).
De två sidorna som ligger bredvid den räta vinkeln (rutan) kallar vi för kateter. Den återstående sidan, som ligger mitt emot den räta vinkeln (hörnet med kvadraten) kallar vi för hypotenusan.
Om man utgår ifrån en viss vinkel i en rätvinklig triangel så kommer det att finnas en katet som är längre bort och en som är närmre. Kateten som är längst bort från vinkeln kallar vi i trigonometriska sammanhang för motstående katet. Den närmare kateten kallar vi för närliggande katet.
Det är viktigt att notera att vilken katet som är närliggande respektive motstående varierar beroende på vilken vinkel man väljer att utgå ifrån. Nedan ser vi en rätvinklig triangel där vi har utgått från vinkeln v som finns i triangelns högra hörn.
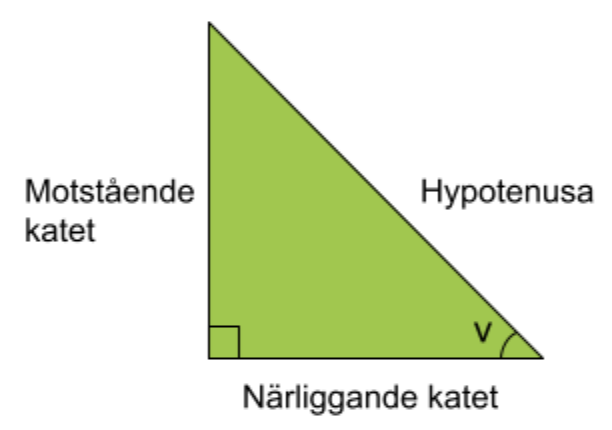
Det är relationen mellan dessa sidor och vinklar som vi kommer gå igenom i det här avsnittet.
Trigonometriska värden i standardvinklar
När du börjar jobba med trigonometri kan det vara en bra idé att skapa en lathund med värdena för sinus, cosinus och tangens i de så kallade standardvinklarna. Dessa vinklar har exakta värden och är därför lättare att komma ihåg.
| Vinkel v | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin v | 0 | 12 | 12 | 32 | 1 |
| cos v | 1 | 32 | 12 | 12 | 0 |
| tan v | 0 | 33 | 1 | 3 | Ej definierbar |
Lägg gärna lathunden i matteboken så att du kan ha den nära till hands när du jobbar med trigonometriska funktioner. På så sätt får du en snabb påminnelse varje gång du öppnar boken vilket kommer hjälpa dig att memorera dem.
Exempel: Bestäm längden av sidan x. Svara i centimeter (cm). Avrunda till en decimal.
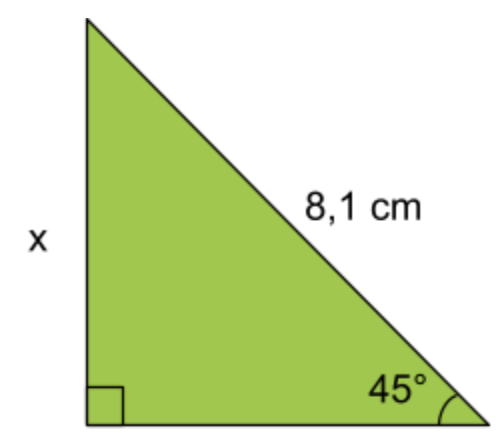
Svar: 5,7\;cm
Lösning: Vi har värdet på en vinkel, som är 45^\circ, och längden av hypotenusan, som är 8,1\;cm. Sett utifrån den 45-gradiga vinkelns perspektiv är sidan x en motstående katet.
Vi vill alltså använda ett samband som inkluderar en vinkel, hypotenusan och en motstående katet. Sinusfunktionen uppfyller detta, eftersom den anger sambandet
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}.
Vi ska därmed använda sinus för att ta reda på vinkeln.
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}Vi sätter in värdena för vår vinkel och hypotenusan. Vi ersätter även den motstående kateten med x.
sin\;45^\circ=\frac{x}{8,1}Vi vill bestämma värdet av x. Därför vill vi att x ska stå ensamt till höger om likamedtecknet. Vi flyttar över 8,1 så att x kan stå ensamt, vilket vi gör genom att multiplicera båda sidorna med 8,1.
sin\;45^\circ=\frac{x}{8,1} {sin\;45^\circ}\cdot{8,1}=\frac{x}{8,1}\cdot{8,1} {sin\;45^\circ}\cdot{8,1}=xNu behöver vi endast bestämma värdet på uttrycket {sin\;45^\circ}\cdot{8,1}. Vi börjar med att hitta ett värde för sin\;45^\circ.
Vi bestämmer värdet av sin\;45^\circ med hjälp av en miniräknare. Vi trycker först på knappen “sin” och knappar sedan in 45. Vi trycker på “enter” och får då värdet på sin\;45^\circ.
sin\;45^\circ\approx0,70711Vi sätter in värdet av sin\;45^\circ i ekvationen x={sin\;45^\circ}\cdot{8,1}.
x={sin\;45^\circ}\cdot{8,1} x={0,70711}\cdot{8,1}Vi beräknar nu produkten {0,70711}\cdot{8,1} i högerled.
x={0,70711}\cdot{8,1}= 5,72756\;cmVi avrundar till en decimal och får att sidan x har längden 5,7\;cm.
Om vi istället vet två av sidorna i en rätvinklig triangel och vill ta reda på en av vinklarna, så använder vi oss av någonting som kallas för en invers trigonometrisk funktion. De inversa funktionerna skrivs som sin^{-1}, cos^{-1} och tan^{-1}, eller arcsin, arccos och arctan.
Precis som med de vanliga trigonometrisk funktionerna så finns de inversa funktionerna inprogrammerade i din miniräknare.
Om vi har en ekvation där vi vill ta reda på vinkeln v, som exempelvis sin\;v=\frac{1}{2}, så kan vi lösa den genom att ta den inversa funktionen av sinus på båda sidorna.
sin\;v=\frac{1}{2} sin^{-1}(sin\;v)=sin^{-1}\frac{1}{2}Termerna sin^{-1} och sin tar ut varandra i vänsterled. Kvar blir vinkeln v.
v=sin^{-1}\frac{1}{2}Vi behöver nu endast beräkna värdet av uttrycket i högerled, sin^{-1}\frac{1}{2}, vilket vi gör med vår miniräknare.
v=sin^{-1}\frac{1}{2}= 30^\circVi får att vinkeln v är 30^\circ.
Vi använder oss alltså av just sin^{-1} eftersom vi har sin\;v i vänsterled. Skulle det stå cos\;v så hade vi använt oss av cos^{-1}.
Exempel: Bestäm vinkeln v. Svara i hela grader (°).
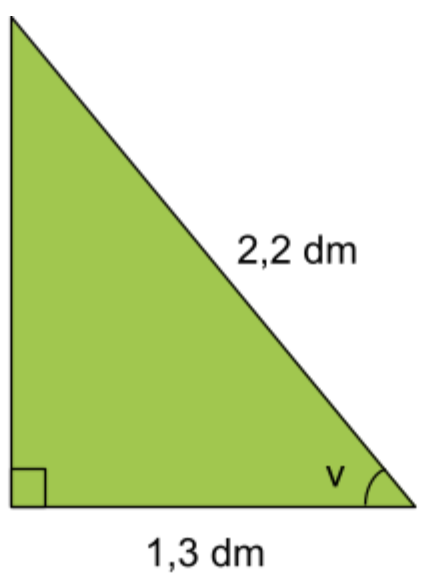
Svar: 54^\circ
Lösning: Vi har längden av en katet, som är 1,3\;dm, och längden av hypotenusan, som är 2,2\;dm. Sett utifrån vinkeln v:s perspektiv är den 1,3\;dm långa kateten en närliggande katet.
Vi vill alltså använda ett samband som inkluderar en vinkel, hypotenusan och en närliggande katet. Cosinusfunktionen uppfyller detta, eftersom den ger sambandet cos\;v=\frac{n\"arliggande\;katet}{hypotenusa}. Vi ska därmed använda cosinus för att ta reda på vinkeln.
cos\;v=\frac{n\"arliggande\;katet}{hypotenusa}Vi sätter in längderna av den närliggande kateten och hypotenusan i sambandet.
cos\;v=\frac{1,3}{2,2}Vi vill att v ska stå ensamt i vänsterled, alltså vill vi flytta över cosinus från vänsterled till högerled. Vi använder därför den inversa cosinusfunktionen, som skrivs cos^{-1}, på båda sidor.
cos^{-1}(cos\;v)=cos^{-1}\frac{1,3}{2,2}Termerna cos^{-1} och cos tar ut varandra i vänsterled. Kvar blir vinkeln v.
v=cos^{-1}\frac{1,3}{2,2}Vi beräknar nu värdet av cos^{-1}\frac{1,3}{2,2} på vår miniräknare.
v=cos^{-1}\frac{1,3}{2,2}\approx 53,78^\circVi avrundar till hela grader och får att vinkeln v är 54^\circ.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Bestäm längden av sidan x. Svara i decimeter (dm). Avrunda till heltal
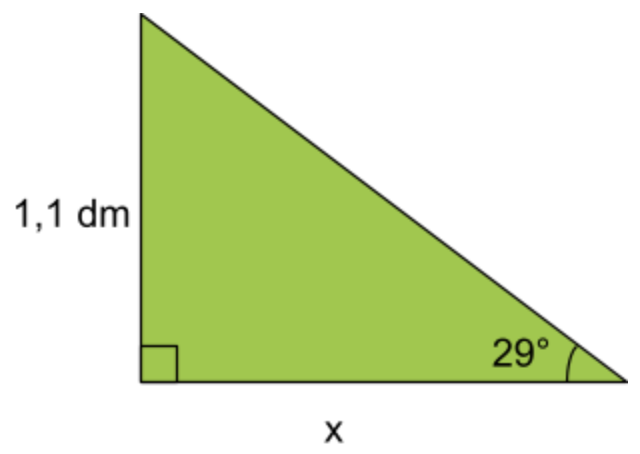
Svarsalternativ 1.1: 1\;dm
Svarsalternativ 1.2: 2\;dm
Svarsalternativ 1.3: 3\;dm
Svarsalternativ 1.4: 4\;dm
Korrekt svar: 2\;dm
Fråga 2: Bestäm längden av sidan a. Svara i centimeter (cm). Avrunda till en decimal.
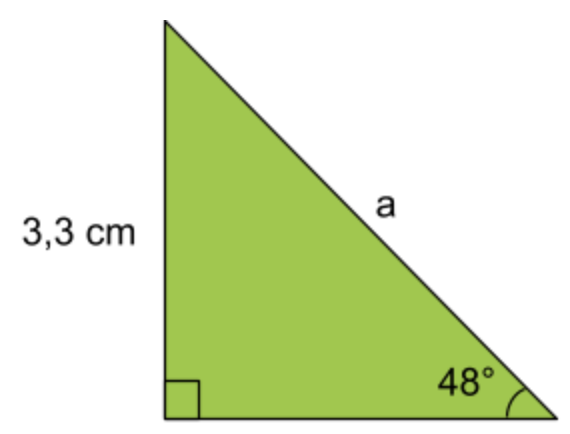
Svarsalternativ 2.1: 2,9\;cm
Svarsalternativ 2.2: 3,9\;cm
Svarsalternativ 2.3: 4,4\;cm
Svarsalternativ 2.4: 4,6\;cm
Korrekt svar: 4,4\;cm
Fråga 3: Beräkna värdet av vinkeln v. Svara i hela grader.
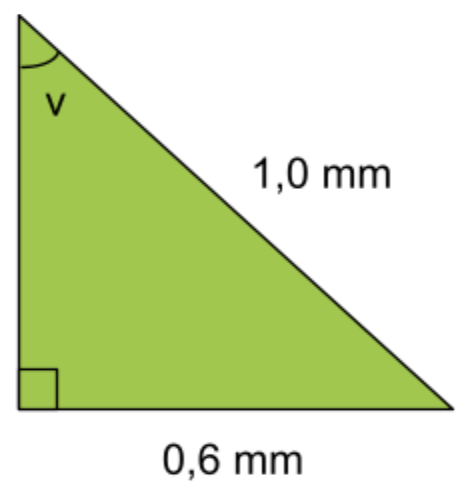
Svarsalternativ 3.1: 34^\circ
Svarsalternativ 3.2: 37^\circ
Svarsalternativ 3.3: 44^\circ
Svarsalternativ 3.4: 54^\circ
Korrekt svar: 37^\circ
Fredrik tipsar
Så kommer du ihåg formlerna

När du börjar jobba med trigonometri kan det vara svårt att hålla reda på vilken formel som ska användas när. Då kan det vara en bra idé att skapa en minnesregel för de olika trigonometriska funktionerna.
Cosinus (cos) – Kossan som håller sig nära: Funktionen cos kan påminna om ordet kossa. En kossa är känd för att vara lat och vill därför hålla sig nära vinkeln. När du vet längden på den närliggande kateten och på hypotenusan vet du alltså att du kan använda cosinussatsen.
Sinus (sin) – Snäll och offrar sig: För att komma ihåg sin kan du tänka på att det börjar på S, precis som snäll. Sinus är snäll och “offrar sig” att gå till den motstående kateten. Därmed kan du räkna ut sin v med hjälp av den motstående kateten och hypotenusan.
Tangens (tan) – Utan hypotenusan: Till sist har vi tan som låter som utan, alltså är det den formeln som kan beräknas utan hypotenusan.
Om du tycker att trigonometrin känns tuff kan du kontakta oss på Allakando och få en erfaren studiecoach som kan hjälpa dig på traven. Alla våra studiecoacher har själva lyckats väldigt bra med sina mattestudier och kan ge dig massor av smarta tips på hur du på bästa sätt jobbar med trigonometri och bemästrar matematiken!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

