Cosinussatsen
Pythagoras sats är bra spännande, men den har ett problem! Den funkar ju bara på rätvinkliga trianglar. Men långt ifrån alla trianglar är rätvinkliga, så då vore det fiffigt om man hade en liknande sats som funkar för vilken triangel som helst. Den satsen kallas cosinussatsen och ser ut så här:
c^2 = a^2 + b^2 - 2ab \cos v
Där v är vinkeln mellan sidorna a & b.
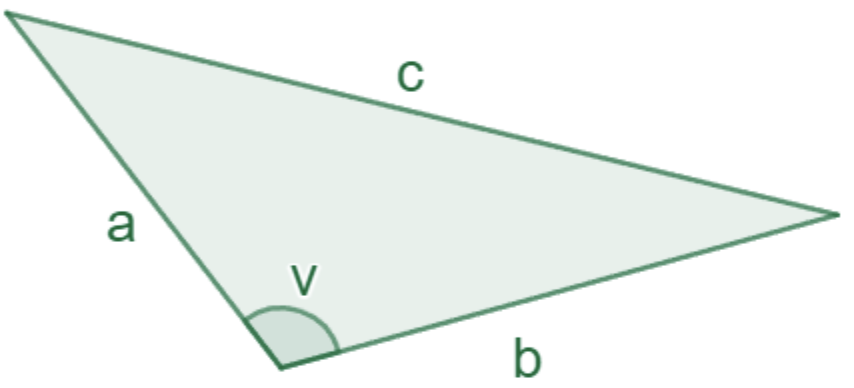
Cosinussatsen kan alltså användas för att hitta den tredje sidan hos en triangel om man kan två sidor och en vinkel, eller hitta vinklarna i en triangel om man har alla tre sidor.
Räkneexempel och förklaringar för cosinussatsen:
Exempel 1: Hitta den tredje sidan c i följande triangel
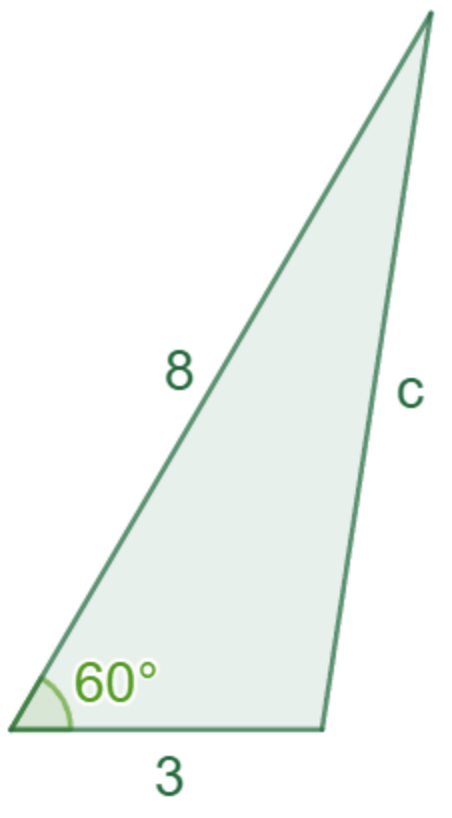
Svar: 7
Förklaring: För att kunna använda cosinussatsen så måste vi först identifiera a,b och v. Vi vet att v är vinkeln som är mellan sidorna a och b, så om vi sätter a= 3, b = 8 och v = 60° så kan vi sedan använda cosinussatsen. Cosinussatsen säger:
c^2 = a^2 + b^2 - 2ab \cos vOm vi nu stoppar in våra värden så får vi:
c^2 = 3^2 + 8^2 - 2 \cdot 3 \cdot 8 \cdot \cos 60^{\circ}Vi räknar ut de olika termerna till:
3^2 = 9, 8^2 = 64, 2 \cdot 3 \cdot 8 = 48 och \cos 60^{\circ} = \frac{1}{2}
Så då får vi:
c^2 = 9 + 64 - 48 \cdot \frac{1}{2}Så
c^2 = 49Tar vi roten ur på båda sidor så får vi:
c = 7Exempel 2: Hitta den markerade vinkeln v i följande triangel
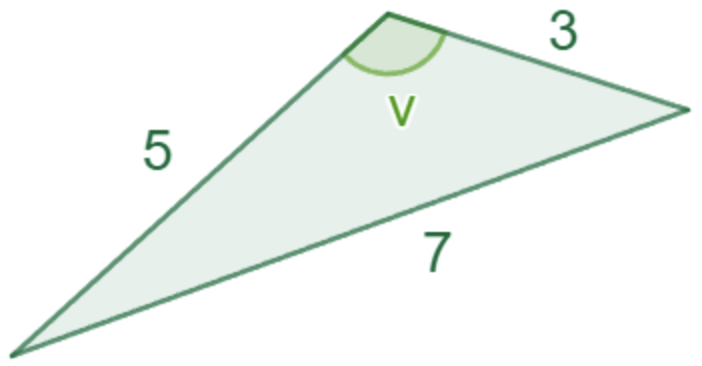
Svar: 120°
Förklaring: Det här är en perfekt uppgift för cosinussatsen! Cosinussatsen säger:
c^2 = a^2 + b^2 - 2ab \cos voch vi vill lösa ut vad v är. Då måste vi först identifiera a, b och c. v är vinkeln mellan sidorna a och b, så då kan vi sätta a=5 och b=3. Då är den sista sidan c=7.
Stoppar vi in alltid i cosinussatsen så får vi:
7^2 = 5^2 + 3^2 - 2 \cdot 5 \cdot 3 \cos vFörenklar vi så får vi:
49 = 25 + 9 - 30 \cos vTar vi minus 25 och minus 9 på båda sidor får vi nu:
15 = - 30 \cos vNästa steg är att dela båda sidor på -30 och då får vi:
\cos v = \frac{15}{-30} = - \frac{1}{2}För att sedan ta reda på vad v är måste vi använda arccos (motsasen till cos). Alltså har vi:
v = \arccos - \frac{1}{2} = 120^{\circ}(Egentligen har ekvationen \cos v = - \frac{1}{2} även lösningen 240°, men en triangel kan inte ha en vinkel större än 180°, så vi vet då att 120° är det korrekta värdet.)
Exempel 3: Hitta den tredje sidan i följande triangel
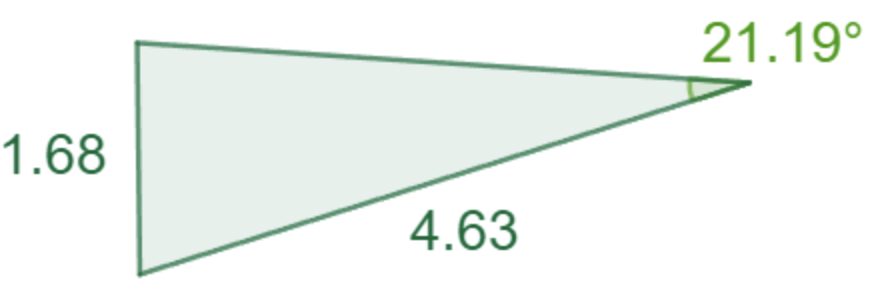
Svar: 4,17 eller 4,46
Förklaring: I det här fallet så ligger vinkeln v mellan sidan 4,63 och den okända sidan. Vi kan alltså sätta a=4,63, c=1,68 och v = 21.19^{\circ} och så vill vi lösa ut b ur cosinussatsen. Stoppar vi in våra värden i cosinussatsen så får vi:
1,68^2 = 4,63^2 + b^2 - 2 \cdot 4,63 \cdot b \cdot \cos 21.19^{\circ}Vi kan beräkna termerna i ekvationen:
1,68^2 = 2,8224 \qquad 4,63^2 = 21,4369 \qquad 2 \cdot 4,63 \cdot \cos 21.19^{\circ} \approx 8.6339vilket gör att ekvationen kan skrivas :
2,8224 = 21,4369 + b^2 - 8,6339 bSom ni ser har vi nu vår okända variabel b i två olika termer och i en av termerna är b i kvadrat. Det här är en andragradsekvation, vilket kan förtydligas genom att skriva den på formen:
b^2 - 8,6339 b + 18,6145 = 0Vi kan nu använda pq-formeln, som ger:
b_1 \approx 4,17 \qquad b_2 \approx 4,46Vi får alltså två lösningar! Det finns två olika trianglar som båda uppfyller måtten som är angivna på bilden, så det här är så långt vi kommer med cosinussatsen.
Övningsuppgifter
Frågor med svarsalternativ:
Rätt svar markeras i grönt.
Fråga 1: Hitta den tredje sidan i följande triangel
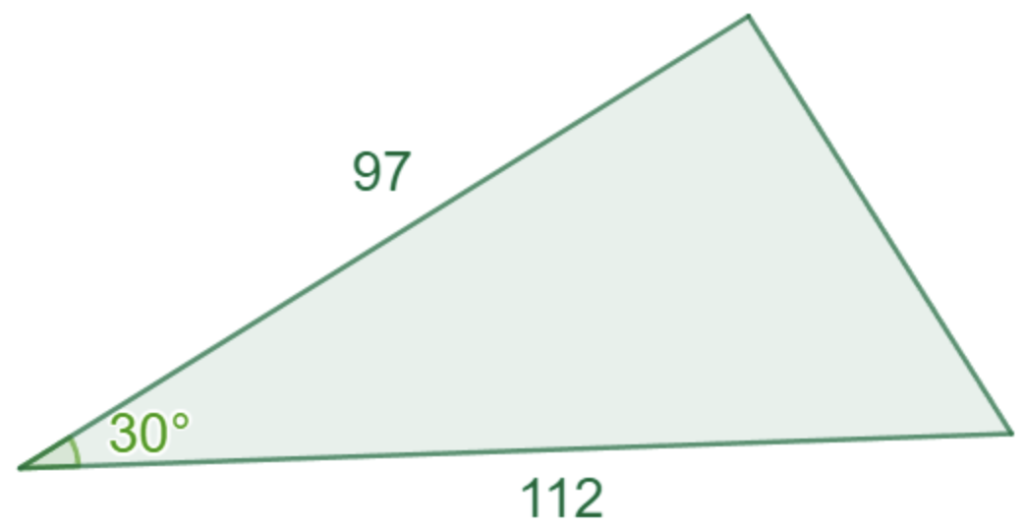
Svarsalternativ 1.1: 51
Svarsalternativ 1.2: 54
Svarsalternativ 1.3: 57
Svarsalternativ 1.4: 60
Fråga 2: Hitta den tredje sidan i följande triangel
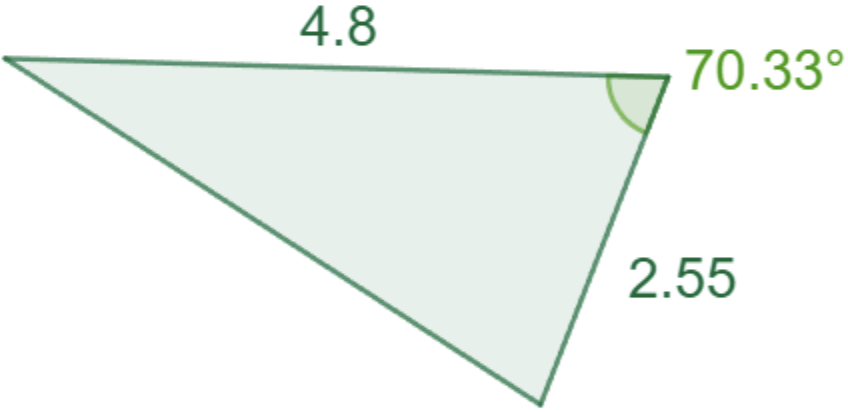
Svarsalternativ 2.1: 3,21
Svarsalternativ 2.2: 3,88
Svarsalternativ 2.3: 4,62
Svarsalternativ 2.4: 5,08
Fråga 3: Beräkna avståndet mellan punkterna i koordinatsystemet:
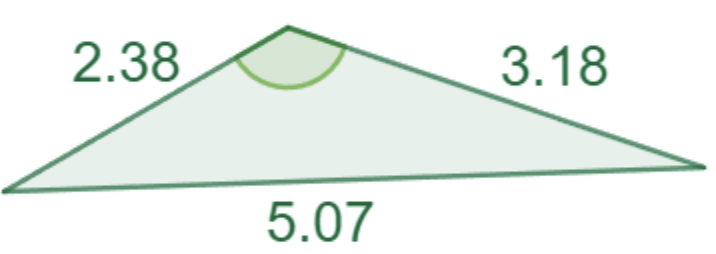
Svarsalternativ 3.1: 95,2°
Svarsalternativ 3.2: 108,25°
Svarsalternativ 3.3: 113,9°
Svarsalternativ 3.4: 131,4°
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

