Standardavvikelse

Mer om standardavvikelse och varians

För att kunna räkna ut standardavvikelse behöver man först behärska varians! Varians är ett mått på hur mycket observationerna i en datamängd skiljer sig från medelvärdet. Man beräknar variansen genom att ta medelvärdet av de kvadrerade avvikelserna från medelvärdet. Det är ett mått på medelvärdet av kvadraten på avvikelserna från medelvärdet. En högre varians indikerar därför större spridning och variation i datamängden.

Hur beräknar man standardavvikelse?

Nu när vi lärt oss varians kan vi hoppa på själva standardsavvikelsen. Standardavvikelsen är kvadratroten av variansen. Att beräkna standardavvikelsen av en samling tal går i 6 steg:

1. Beräkna medelvärdet för talen
2. Ta talen minus medelvärdet
3. Kvadrera alla tal
4. Lägg ihop dem
5. Dela på antalet tal
6. Ta roten ur

Dessa steg kan sammanfattas med formeln:

\sigma= \sqrt\frac{\sum (x-m)^{2}}{n}

\sigma är standardavvikelsen, x är mätvärden, m är medelvärdet, n är antal mätvärden, och \sum innebär att vi lägger ihop alla värden.

Låt oss se hur det här fungerar i praktiken.

Räkneexempel och förklaringar för standardavvikelse:

Exempel: Mikael mätte hur lång tid bussen var försenad varje dag i en vecka. Han fick resultatet: 5 min, 0 min, 3 min, 2 min, 0 min. Beräkna standardavvikelsen!

Svar: 1,9 min

Förklaring: Vi börjar med att beräkna medelvärdet för värdena:

\frac{5+0+3+2+0}{5} \textrm{min} = \frac{10}{5}\textrm{min = 2 min}

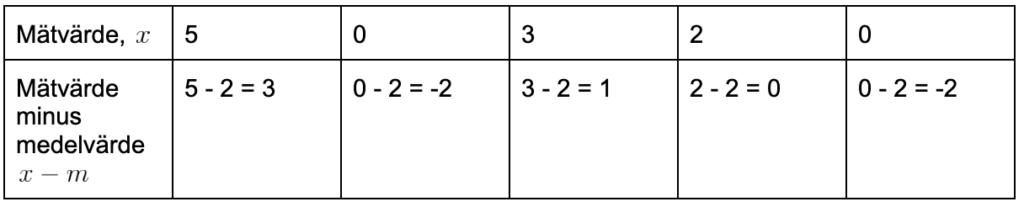
Härnäst vill vi kvadrera talen:

Nu vill vi lägga ihop de tal vi har fått och dela på antalet:

\frac{\sum (x - m)^{2}}{n} = \frac{9+4+1+0+4}{5} = \frac{18}{5} = 3,6

Och till sist vill vi ta roten ur:

\sigma= \sqrt\frac{\sum (x-m)^{2}}{n} = \sqrt{3,6} \approx 1,9

Så standardavvikelsen är 1,9 minuter!

---

Exempel 2: Anastasia undersöker hur många prickar nyckelpigor har! Hon hittar nyckelpigor med prickar 7, 3, 2, 6, 4, 0, 3, 7. Beräkna standardavvikelse!

Svar: 2,34 prickar

Förklaring: Vi börjar med att beräkna medelvärdet för värdena:

\frac{7+3+2+6+4+0+3+7}{8} = \frac{32}{8} = 4

Om vi nu tar har varje tal minus medelvärdet så får vi:

Härnäst vill vi kvadrera talen:

Nu vill vi lägga ihop de tal vi har fått och dela på antalet:

\frac{\sum (x - m)^{2}}{n} = \frac{9+1+4+4+0+16+1+9}{8} = \frac{44}{5} = 5,5

Och till sist vill vi ta roten ur:

\frac{\sum (x - m)^{2}}{n} = \sqrt{5,5} \approx 2,34

Så standardavvikelsen är 2,34 prickar!