Reella tal
Inom matematik finns det flera olika typer av tal. Vi kallar de olika sorters tal för olika talmängder. En sådan talmängd är de reella talen. De reella talen är alla tal som kan skrivas som ett heltal, ett bråktal och/eller ett decimaltal.
Vad är reella tal?
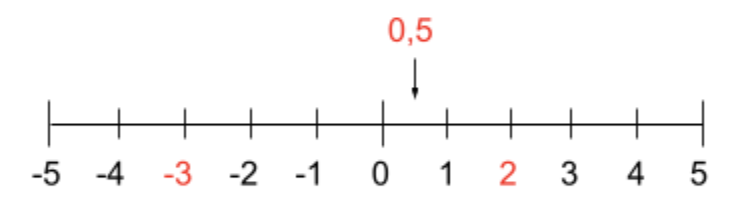
Reella tal kallas de tal som vi vardagligt sett brukar räkna som tal. De reella talen är tal som vi kan placera på en tallinje. Nedan ser vi ett exempel på en tallinje som går från 5 till -5.

Vi upptäcker att tal som exempelvis -3, 0,5 och 2 alla kan placeras på tallinjen. Därmed vet vi att -3, 0,5 och 2 är reella tal.
Räkneexempel och förklaringar
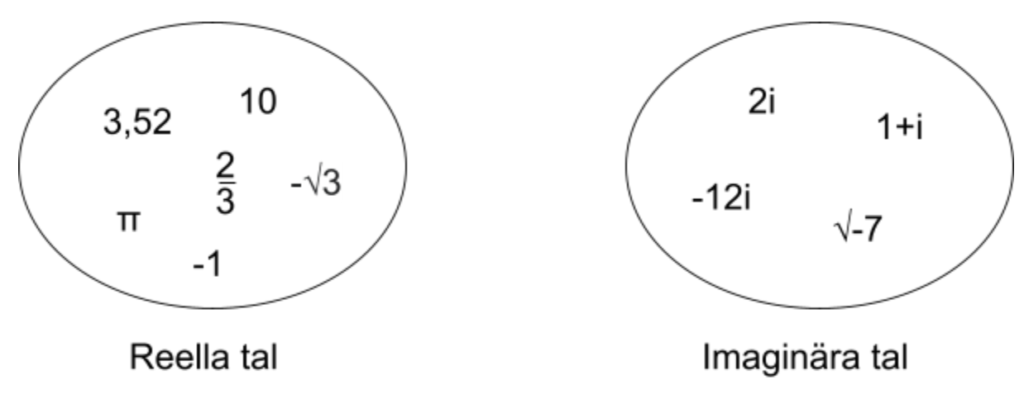
Som vi nämnt är de allra flesta tal reella. De enda tal som inte tillhör gruppen reella tal är tal som innehåller en rot ur ett negativt tal. \sqrt{-4} är ett exempel på ett icke-reellt tal. Vi ser detta eftersom vi inte kan passa in [/latex]\sqrt{-4}[/latex] på en tallinje.
Tal som är icke-reella kallas även för imaginära tal. Ofta när vi skriver de imaginära talen ersätter vi minustecknet med ett i som vi placerar längst bak i talet.
\sqrt{-4} kan på så vis skrivas som \sqrt{4}i=2i.
Vi vet därmed att tal som innehåller i, alltså innehåller en rot ur ett negativt tal och på så vis är även dessa tal imaginära. Tal som består av både en reell del och en imaginär del, som exempelvis 1+3i hör till de imaginära talen.
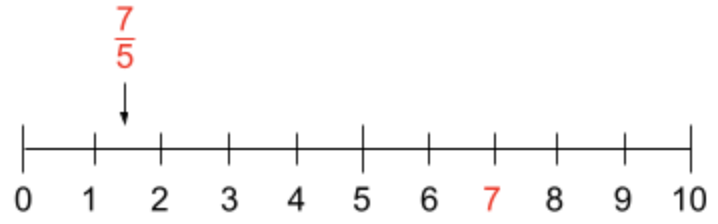
Exempel: Vilket/vilka av talen \sqrt{-3}, \frac{7}{5} och 7 är reella?
Svar: \frac{7}{5} och 7
Lösning: Vi kommer ihåg att de enda tal som inte är reella är de tal som innehåller en negativ rot eller i. Vi undersöker därmed om talen \sqrt{-3}, \frac{7}{5} och 7 innehåller någon av dessa två delar.
Vi upptäcker direkt att \sqrt{-3} är en rot ur ett negativt tal. Detta innebär att \sqrt{-3} är imaginärt och på så vis inte reellt.
Vidare ser vi att \frac{7}{5} och 7 inte innehåller en negativ rot eller i. Därmed vet vi att dessa tal är reella.
Vi kan ytterligare visa att \frac{7}{5} och 7 är reella genom att placera talen på en tallinje, vilket vi inte kan göra med \sqrt{-3}.
Exempel: Är 6+5 i ett reellt tal eller ett imaginärt tal?
Svar: 6+5i är ett imaginärt tal.
Lösning: Vi ser att talet 6+5i består av en reell del, 6, och en imaginär del, 5i. Om ett tal innehåller både en reell del och en imaginär del så räknas talet som imaginärt. Därför är 6+5 i ett imaginärt tal.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Vilket/vilka av talen π, 3,3 och 6i är reella?
Svarsalternativ 1.1: 3,3
Svarsalternativ 1.2: π och 3,3
Svarsalternativ 1.3: 3,3 och 6
Svarsalternativ 1.4: π, 3,3 och 6
Korrekt svar: π och 3,3
Fråga 2: Vilket av följande tal är reellt?
Svarsalternativ 2.1: \sqrt{-11}
Svarsalternativ 2.2: \frac{i}{3}
Svarsalternativ 2.3: 2+3i
Svarsalternativ 2.4: -\frac{7}{5}
Korrekt svar: -\frac{7}{5}
Fråga 3: Vilket av följande tal är imaginärt?
Svarsalternativ 3.1: -\sqrt{2}
Svarsalternativ 3.2: \sqrt{2}
Svarsalternativ 3.3: \sqrt{-2}
Svarsalternativ 3.4: -2
Korrekt svar: \sqrt{-2}
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla nivåer
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

