Likbent triangel
Det finns många typer av trianglar och en av de mer spännande typer är den likbenta triangeln. En likbent triangel är en triangel där två av sidorna är lika långa! De två sidorna som är lika långa kallas då för benen hos triangeln, och den kallas likbent just eftersom benen är lika långa. Man kan göra många spännande saker med likbenta trianglar – till exempel så är sidorna på en pyramid likbenta trianglar!
En följd av att två sidor är lika långa är att en likbent triangel alltid har två vinklar som är lika stora! De två vinklar som är lika stora kallas för basvinklar.
Skillnaden mellan likbent triangel och liksidig triangel
Det är lätt att man blandar ihop en likbent triangel med en liksidig triangel! Men va där egentligen skillnaden?
En likbent triangel är en triangel där två av sidorna är lika långa, vilket resulterar i två lika stora vinklar vid basen. Den tredje sidan, som kallas för höjden, kan vara av en annan längd. En likbent triangel har alltså två lika sidor och två lika vinklar.
Å andra sidan är en liksidig triangel en triangel där alla tre sidor är lika långa, och alla tre vinklar är lika stora, nämligen 60 grader. Det betyder att en liksidig triangel är symmetrisk och har tre lika sidor och tre lika vinklar.
Räkneexempel och förklaringar för likbenta trianglar
Exempel: Vilka av trianglarna i bilden är likbenta? Trianglarnas sidlängder är angivna i bilden.
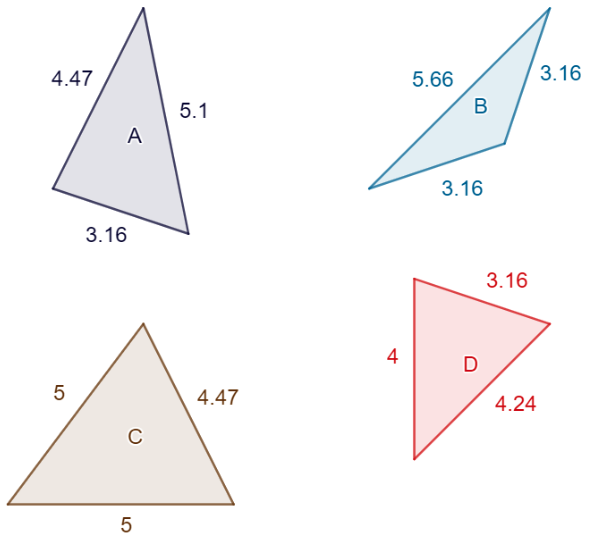
Svar: B och C
Förklaring: En likbent triangel ska ha två sidor med samma längd. Vi kollar först på triangel A, som har sidlängderna 3,16, 4,47 och 5,1. Ingen av de tre sidlängderna är alltså lika, så triangeln A är inte en likbent triangel.
Kollar vi nu på triangel B, så ser vi att den har sidlängderna 3,16, 3,16 och 5,66. Den har alltså två sidor som har längden 3,16. Eftersom triangeln har två sidor med samma längd så är den en likbent triangel!
Låt oss nu kolla på triangel C. Den har sidlängderna 4,77, 5 och 5. Nu ser vi igen att den har två sidor som är lika långa, eftersom tvp av sidorna har längden 5. Alltså är även triangel C en likbent triangel.
Till sist kollar vi på triangel D. Den har sidlängderna 3,16, 4 och 4,24. Inga av de tre längderna är lika med varandra, så triangel D är inte likbent.
Exempel: Vilka av trianglarna i bilden är likbenta? Trianglarnas vinklar är angivna i bilden.
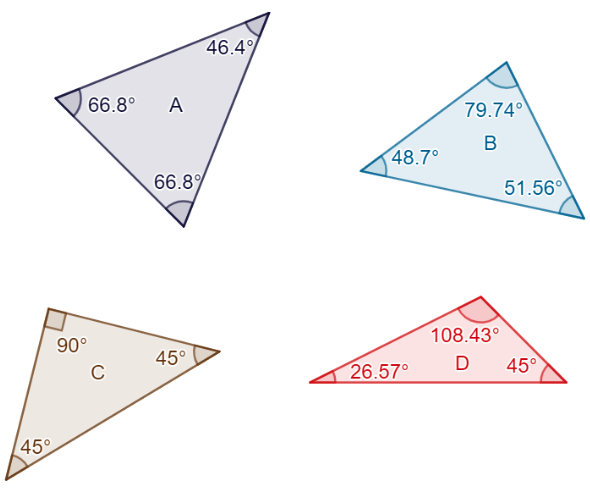
Svar: A och C
Förklaring: En likbent triangel har alltid två vinklar som är lika stora. Vi börjar med att undersöka triangel A. Den har vinklarna 46,4°, 66,8° och 66,8°. Den har alltså två vinklar som är lika stora, 66,8°, så triangeln är likbent.
Nu kollar vi på triangel B. Den har vinklarna 48,7°, 51,6° och 79,74°. Inga av de vinklarna är lika stora, så triangel B är inte likbent.
Vi kollar nu på triangel C, som har vinklarna 45°, 45° och 90°. Vi ser att två vinklar är 45°, så triangeln är likbent!
Till sist kollar vi på triangel D, med vinklarna 26,57°, 45° och 108,43°. Här är ingen av vinklarna samma som någon annan vinkel, så triangeln är inte en likbent triangel.
Exempel: I en likbent triangel, om basvinklarna är 40°, vad är den tredje vinkeln?
Svar: 100°
Förklaring: Nu måste vi komma ihåg en viktig egenskap hos en triangel: lägger man ihop alla vinklar i triangeln så får man 180°. I det här fallet ska alltså \text{basvinkel} + \text{basvinkel} + \text{tredje vinkeln} = 180°.
Men vi har ju att basvinklarna är 40°, vilket ger 40° + 40° + \text{tredje vinkel} = 180°
Vi har nu en ekvation för den sökta vinkeln! Vi kan förenkla vänstersidan genom att lägga ihop de två 40°
80° + \text{tredje vinkel} = 180°Vi vill nu ha bort 80° från vänstersidan, så vi tar minus 80° från båda sidor 80° + \text{tredje vinkel} - 80° = 180° - 80° vilket ger \text{tredje vinkel} = 100°
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Vilken av trianglarna i bilden är inte likbent?
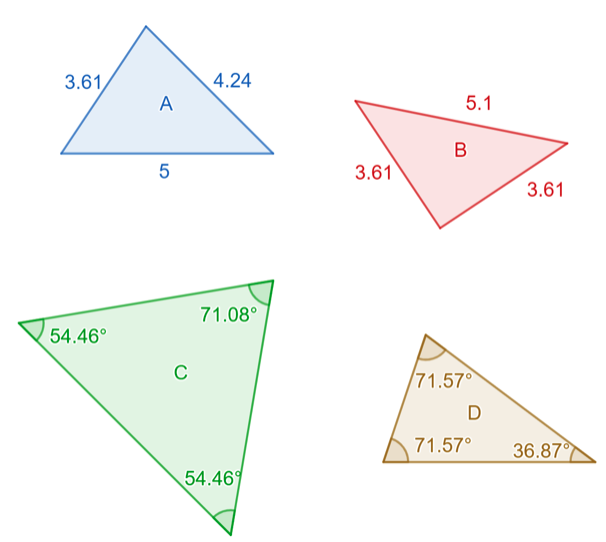
Svarsalternativ 1.1: A (rätt)
Svarsalternativ 1.2: B
Svarsalternativ 1.3: C
Svarsalternativ 1.4: D
Fråga 2: Basvinklarna i en likbent triangel är 70°. Vad är tredje vinkeln?
Svarsalternativ 2.1: 20°
Svarsalternativ 2.2: 30°
Svarsalternativ 2.3: 40° (rätt)
Svarsalternativ 2.4: 50°
Fråga 3: Vad är basvinklarna i en likbent triangel om den tredje vinkeln är 120°?
Svarsalternativ 3.1: 30° (rätt)
Svarsalternativ 3.2: 45°
Svarsalternativ 3.3: 60°
Svarsalternativ 3.4: 90°
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla åldrar
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

