Integral
Integraler är ett spännande koncept, som bygger på att man lägger ihop massor av funktionsvärden. Effekten av det är att man ackumulerar funktionsvärdena. Som exempel, om man fyller en kanna med vatten så kan man ha en funktion som beskriver vattenflödet (liter/sekund). Integralen av funktionen ger då hur mycket vatten som totalt har hamnat i kannan under någon tidsperiod – ackumulationen av vattenflödet. Integraler betecknas \int_a^b f(x) dx
f(x) är funktionen vi integrerar, och a och b är nedre och övre gräns för integralen – de beskriver mellan vilka x-värden vi lägger ihop funktionsvärden.
En viktig egenskap hos integraler är hur de förhåller sig till derivator. Vi har nämligen den väldigt viktiga satsen \int_a^b f'(x) dx = f(b) - f(a) vilket med ord säger att om vi ackumulerar små förändringar f'(x) mellan x=a och x=b, så får vi den totala förändringen f(b) - f(a)
När man vill beräkna integraler så brukar man istället skriva med primitiva funktioner: \int_a^b f(x) dx = F(b) - F(a)
Räkneexempel och förklaringar för integraler
Exempel: \int_0^6 (x-2) dx
Svar: 6
Förklaring: När man vill beräkna en integral av en funktion, så måste man först hitta den primitiva funktionen till integralen! I det här fallet har vi funktionen f(x) = x-2 som vi vill hitta den primitiva funktionen på. Vi kan använda regeln att g(x) = x^a \implies G(x) = \frac{x^{a+1}}{a+1}
Detta ger att vår funktion har den primitiva funktionen F(x) = \frac{x^2}{2} - 2x.
Bra! Nu behöver vi veta vad vi ska stoppa in för värden i den primitiva funktionen. Vi har ju att \int_a^b f(x) = F(b) - F(a) så det vi måste göra nu är att identifiera a och b. Den nedre gränsen av integralen är a, vilket i uppgiften är 0, så vi har att a = 0. Integralens övre gräns är b, vilket i uppgiften är 6.
Alltså har vi b=6. Kvar är nu bara att stoppa in dessa i den primitiva funktionen: F(b) = F(6) = \frac{6^2}{2} - 2 \cdot 6.
Vi börjar med att förenkla första termen:
\frac{6^2}{2} = \frac{36}{2} = 18.
Vi förenklar nu andra termen:
2 \cdot 6 = 12Så F(b) är alltså F(6) = 18 - 12 = 6.
Nu behöver vi hitta F(a): F(a) = F(0) = \frac{0^2}{2} - 2 \cdot 0.
Båda termerna här blir ju 0! Alltså har vi att F(a) = F(0) = 0.
Därför blir F(b) - F(a) = 6 - 0 = 6 vilket är svaret!
Exempel: Beräkna den markerade arean i figuren
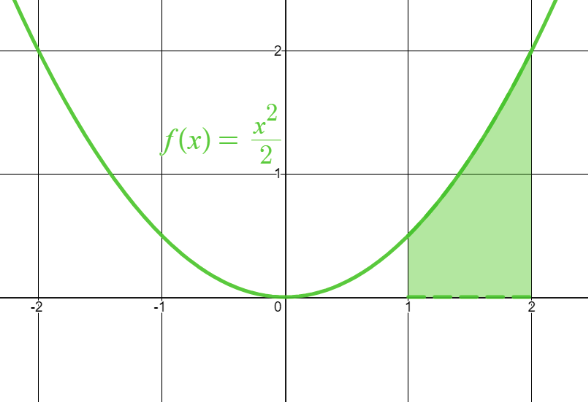
Svar: \frac{1}{6}
Förklaring: Vi vill beräkna arean mellan kurvan av en funktion och x-axeln. Det här är ett utmärkt användningsområde för integraler! Vi har att den allmänna formen \int_a^b f(x) dx beräknar arean mellan kurvan f(x) och x-axeln, mellan x-värdena x=a och x=b.
I det här fallet så har vi att arean är mellan x=1 och x=2, så var den undre gränsen på integralen a=1 och den övre gränsen b=2. Med funktionen enligt figuren vill vi alltså beräkna \int_1^2 \frac{x^2}{2}dx.
Vi behöver nu hitta den primitiva funktionen, vilket vi kan göra med regeln g(x) = x^a \implies G(x) = \frac{x^{a+1}}{a+1} så vi får att den primitiva funktionen är F(x) = \frac{x^3}{3}/2 = \frac{x^3}{6}.
Vi kan nu stoppa in a och b i den primitiva funktionen:
F(b) = F(2) = \frac{2^3}{6} = \frac{8}{6} och F(a) = F(1) = \frac{1^3}{6} = \frac{1}{6}
Så den sökta arean blir \int_1^2 \frac{x^2}{2}dx = F(2) - F(1) = \frac{8}{6} - \frac{1}{6} = \frac{7}{6}
Exempel: Beräkna den markerade arean i figuren
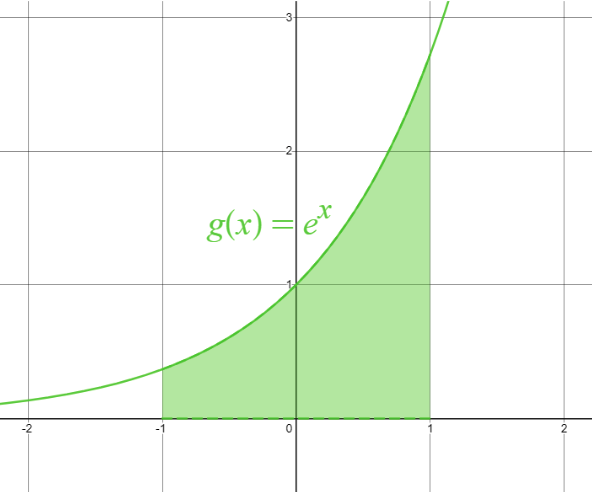
Svar: 2,35
Förklaring: Vi vill beräkna arean, så vi ska igen beräkna en integral! För att göra det behöver vi ta reda på den primitiva funktionen till f(x) = e^x, som det finns en regel för som säger F(x) = e^x
Vi behöver också ta reda på a och b. Den undre gränsen ser vi från bilden är a=-1, och den övre gränsen är b=1. Vi får då att arean är lika med \int_{-1}^1 e^x dx = F(1) - F(-1)
Vi har att F(1) = e^1 = e och F(-1) = e^{-1}
Så arean mellan kurvan och x-axeln är F(1) - F(-1) = e - e^{-1}
Vi kan såklart knappa in det i räknaren också, så får vi att arean är e - e^{-1} \approx 2,35
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Beräkna integralen \int_{0}^2 x dx
Svarsalternativ 1.1: 1
Svarsalternativ 1.2: 2 (rätt)
Svarsalternativ 1.3: 3
Svarsalternativ 1.4: 4
Fråga 2: Beräkna integralen \int_{-2}^0 x^3 dx
Svarsalternativ 2.1: -4
Svarsalternativ 2.2: -2
Svarsalternativ 2.3: 2
Svarsalternativ 2.4: 4 (rätt)
Fråga 3: Vad är arean i bilden?
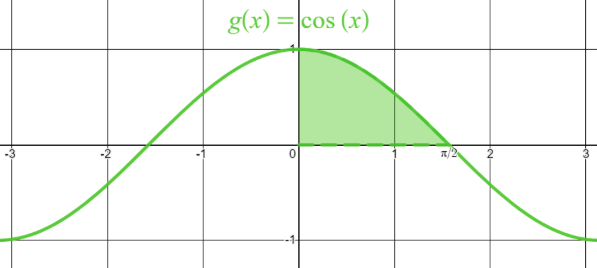
Svarsalternativ 3.1: -1
Svarsalternativ 3.2: 0
Svarsalternativ 3.3: 1
Svarsalternativ 3.4: \pi/2
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla åldrar
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

