Omkrets cirkel – Räkna ut omkretsen på en cirkel
En cirkel är en figur som är helt rund och alltså inte har några vinklar eller sidor. Cirkeln utgår från en medelpunkt som sitter precis i mitten av figuren. Medelpunkten markeras med en prick samt ett M eller O.
Vad är en cirkels omkrets?
När vi talar om omkretsen hos en figur syftar vi på längden runt dess yttre kant. För figurer med sidor, som en triangel, lägger vi helt enkelt till längden av varje sida för att få omkretsen. Men när det kommer till en cirkel, som inte har några distinkta sidor, blir det lite annorlunda.
För att förstå omkretsen av en cirkel kan du tänka dig att du har ett rep som du kan vira runt cirkeln. Sedan kan du bara mäta hur långt repet är. Det är dock inte alltid så lätt att mäta kring cirklar på det sättet men som tur är finns det en matematisk lösning. Genom att använda cirkelns radie eller diameter kan vi räkna ut omkretsen utan att behöva mäta.
Radie och diameter på en cirkel
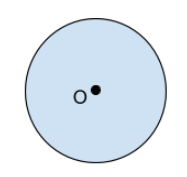
Avståndet från cirkelns mitt till dess yttre kant kallas för radien. Vi betecknar radien med ett r och oavsett vilken punkt på cirkelns kant vi väljer att dra radien till kommer den vara densamma.
Avståndet mellan två motsatta punkter på cirkelns kant kallas för diametern. Diametern betecknar vi med ett d. Det är viktigt att diametern alltid är en rak linje och att den går genom medelpunkten.
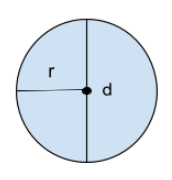
Diametern är därmed alltid dubbelt så stor som radien. Vi kan alltså säga att en cirkels radie och diameter följer sambandet:
d={2}\cdot{r}Hur räknar man ut omkretsen på en cirkel?
Att beräkna cirkelns omkrets är lite annorlunda eftersom vi inte kan mäta i figuren, men det följer ett visst samband.
O={\pi}\cdot{d}Vi kan även skriva cirkelns omkrets som O={2}\cdot{\pi}\cdot{r} eftersom vi vet att d={2}\cdot{r}.
I sambandet är d cirkelns diameter och r cirkelns radie. Pi är ett tal som ofta dyker i samband med cirklar. Pi har oändligt många decimaler, men för att göra det något lättare att skriva brukar vi avrunda det till 3,14. Vi skriver pi med tecknet π.
Vi definierar π som cirkelns omkrets delat på cirkelns diameter.
\frac{cirkelns\;omkrets}{cirkelns\;diameter}={\pi} \approx\ 3,14Formel för att räkna ut omkretsen på en cirkel
Formeln för att beräkna omkretsen av en cirkel är:
Omkrets = 2πr
där π (pi) är en matematisk konstant som ungefär motsvarar 3,14159 och r är cirkelns radie.
Om du endast vet diametern (d) av cirkeln och inte radien kan du istället använda formeln:
Omkrets = πd
Kom ihåg! Radien är avståndet från cirkelns mittpunkt till vilken som helst punkt på ytterkanten, medan diametern är avståndet mellan två punkter på ytterkanten som går igenom cirkelns mittpunkt. Radien är hälften av diametern.
För att använda formeln för omkretsen av en cirkel, mäter du först radien eller diametern. Om du har cirkelns radie multiplicerar du den med 2π för att få omkretsen. Om du har cirkelns diameter multiplicerar du den istället med π för att få omkretsen.
Räkneexempel för en cirkels omkrets
Låt oss säga att vi har en cirkel med radien 3 cm och vi vill beräkna omkretsen. Vi ska svara i cm.
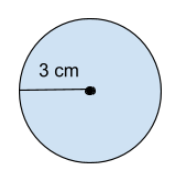
Vi använder oss av sambandet O={2}\cdot{\pi}\cdot{r} för att beräkna omkretsen. Vi börjar med att sätta in värdet för radien.
O={2}\cdot{\pi}\cdot{r}= {2}\cdot{\pi}\cdot{3}Vi multiplicerar nu talen 2 och 3 med varandra.
{2}\cdot{\pi}\cdot{3}= {6}\cdot{\pi}\;cmNär vi har π i en uträkning skriver vi inte ut dess decimaler i svaret. Vi svarar alltså att omkretsen för cirkeln är {6}\cdot{\pi}\;cm
Arean av en cirkel beror också på cirkelns radie samt π, men sambandet ser lite annorlunda ut:
A={\pi}\cdot{r^2}I sambandet är r^2 cirkelns radie multiplicerat med sig självt. Om vi har att radien är 3 cm får vi alltså att r^2=3^2={3}\cdot{3}=9\;cm. π är ett tal som avrundas till ungefär 3,14.
Låt oss säga att vi har en cirkel med radien 5 dm.
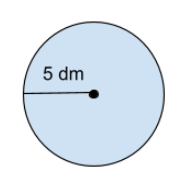
Vi börjar med att sätta in värdet för radien i vårt samband.
A={\pi}\cdot{r^2}= {\pi}\cdot{3^2}Vi börjar med att förenkla termen {3^2}.
{\pi}\cdot{3^2}= {\pi}\cdot{3}\cdot{3}= {\pi}\cdot{9}\;dm^2Vi får alltså att arean för cirkeln är {9}\cdot{\pi}\;dm^2.
Få en videogenomgång
Bli expert på att räkna ut cirkelns omkrets med den här videogenomgången.
Övningsuppgifter – omkrets cirkel
Frågor med svarsalternativ:
Fråga 1: Beräkna cirkelns omkrets. Svara i centimeter (cm).
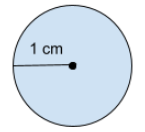
Svarsalternativ 1: {2}\cdot{\pi}\;cm
Svarsalternativ 2: {4}\cdot{\pi}\;cm
Svarsalternativ 3: {5}\cdot{\pi}\;cm
Svarsalternativ 4: {8}\cdot{\pi}\;cm
Korrekt svar: {2}\cdot{\pi}\;cm
Fråga 2: Beräkna cirkelns omkrets. Svara i meter (m).
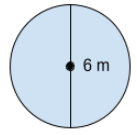
Svarsalternativ 1: {2}\cdot{\pi}\;m
Svarsalternativ 2: {4}\cdot{\pi}\;m
Svarsalternativ 3: {6}\cdot{\pi}\;m
Svarsalternativ 4: {9}\cdot{\pi}\;m
Korrekt svar: {6}\cdot{\pi}\;m
Fråga 3: Beräkna cirkelns omkrets. Svara i decimeter (dm).
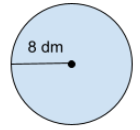
Svarsalternativ 1: {9}\cdot{\pi}\;dm^2
Svarsalternativ 2: {25}\cdot{\pi}\;dm^2
Svarsalternativ 3: {36}\cdot{\pi}\;dm^2
Svarsalternativ 4: {64}\cdot{\pi}\;dm^2
Korrekt svar: {64}\cdot{\pi}\;dm^2
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

