Avståndsformeln
Avståndsformeln är en formel för att räkna ut avståndet mellan två punkter i ett koordinatsystem, genom att använda punkternas koordinater. Till exempel så använder GPS avståndsformeln för att beräkna var på Jorden man befinner sig, utifrån hur långt bort man är från olika satelliter.
Om man har ena punkten (x_1, y_1) och andra punkten (x_2, y_2) så säger avståndsformeln att distansen d mellan punkterna är:
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
Räkneexempel och förklaringar för avståndsformeln:
Exempel 1: Vad är avståndet mellan punkten (1,2) och punkten (7, 4)?
Svar: 13
Förklaring: För att hitta avståndet så vill vi använda avståndsformeln. För att kunna använda avståndsformeln så måste vi veta vad x_1, x_2, y_1 och y_2 är. Då kollar vi först på den ena punkten, som har koordinaterna:
(x_1, y_1) = (1,2)Alltså har vi x_1 = 1 och y_1 = 2 . Om vi stoppar in dem i avståndsformeln så får vi:
d = \sqrt{(x_2 - 1)^2 + (y_2 - 2)^2}Sedan kollar vi på den andra punkten som har koordinaterna:
(x_2, y_2) = (13, 7)Alltså har vi x_2 = 13 och y_2 = 7. Vi kan nu också stoppa in dem i avståndsformeln:
d = \sqrt{(13 - 1)^2 + (7 - 2)^2}Vi är nu redo att räkna ut vad avståndet blir. Vi börjar med att förenkla parenteserna:
(13 - 1) = 12, \qquad (7-2) = 5Då kan vi skriva om uttrycket för avståndet d till:
d = \sqrt{12^2 + 5^2}Sedan så tar vi:
12^2 + 5^2 = 144 + 25 = 169Så att avståndet är:
d = \sqrt{169}Och så till sist vill vi beräkna roten ur, och då får vi:
d = 13Vilket är svaret!
Exempel 2: Beräkna avståndet mellan punkterna i koordinatsystemet:
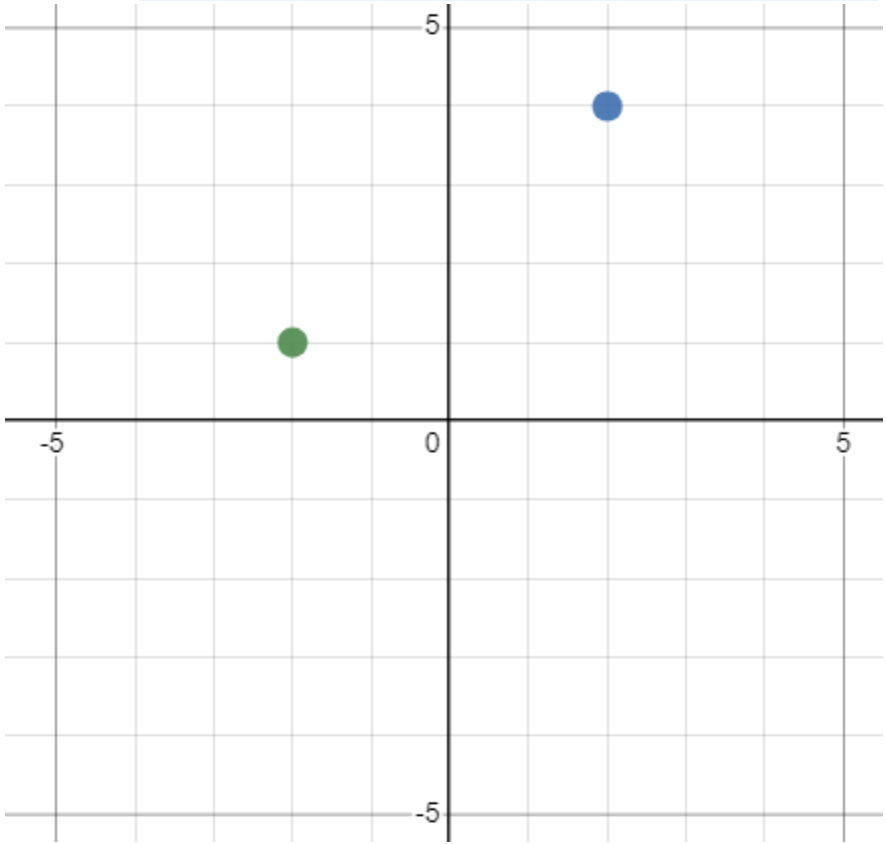
Svar: 5
Förklaring: För att kunna använda avståndsformeln så måste vi först veta vad punkterna har för koordinater. Den gröna punkten har ett x-värde på x_1 = -2 och ett y-värde på y_1 = 1. Den blå punkten har ett x värde på x_2 = 2 och ett y-värde på y_2 = 4. Stoppar vi in dessa i avståndsformeln så får vi:
d = \sqrt{(2 - (-2))^2 + (4 - 1)^2}Vi vill nu förenkla det här, och vi börjar med att utföra beräkningarna inuti parenteserna:
d = \sqrt{4^2 + 3^2}Sedan fortsätter vi genom att utföra upphöjt till två:
d = \sqrt{16 + 9}Sedan lägger vi ihop talen inuti roten ur tecknet:
d = \sqrt{25}Och till sist tar vi roten ur:
d = 5Så svaret är 5.
Övningsuppgifter
Frågor med svarsalternativ:
Rätt svar markeras i grönt.
Fråga 1: Vad är avståndet mellan punkten (0,2) och punkten (15, 10)?
Svarsalternativ 1.1: 8
Svarsalternativ 1.2: 15
Svarsalternativ 1.3: 17
Svarsalternativ 1.4: 20
Fråga 2: Vad är avståndet mellan punkten (1,1) och punkten (2, 2)?
Svarsalternativ 2.1: 1
Svarsalternativ 2.2: \sqrt{2}
Svarsalternativ 2.3: \sqrt{3}
Svarsalternativ 2.4: 2
Fråga 3: Beräkna avståndet mellan punkterna i koordinatsystemet:
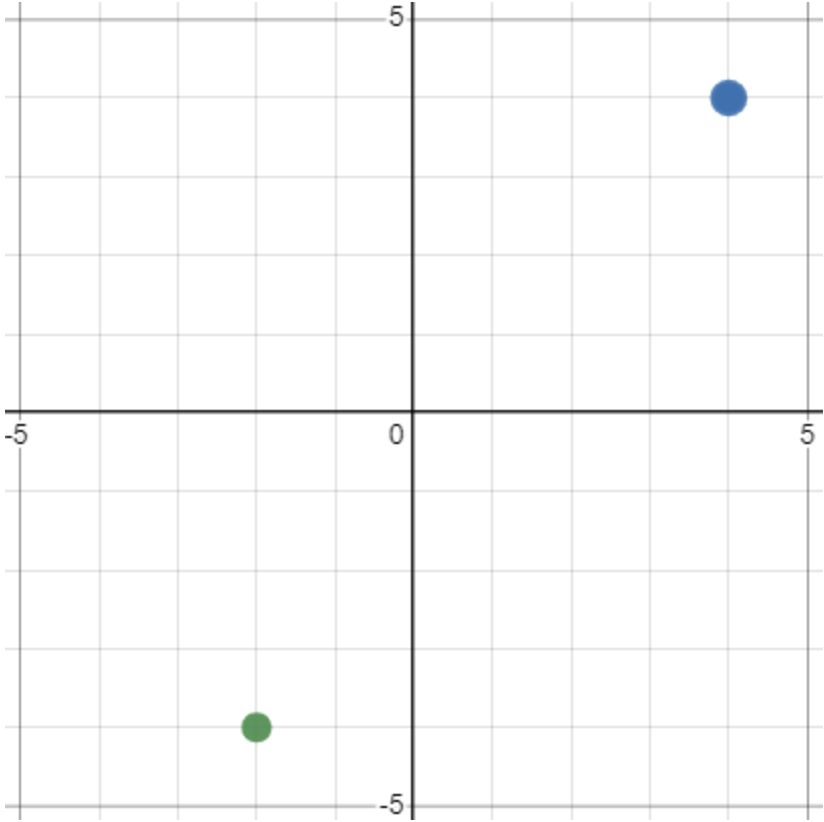
Svarsalternativ 3.1: 6
Svarsalternativ 3.2: 8
Svarsalternativ 3.3: 10
Svarsalternativ 3.4: 12
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

