Sammanfattning av nationella provet i matte 3

Nationella provet för matte 3b och 3c består av tre stycken skriftliga delprov. På delproven testas bland annat optimeringsproblem, förändringar och extremvärden. Provet lär också fokusera på algebra och funktioner. För dig som läser 3c kan det vara bra att hålla koll på trigonometri. Här kommer en sammanfattning av det allra viktigaste!

/Fredrik Fridlund på Allakando

Sammanfattning av nationella provet i matte 1

Ekvationer & Funktioner

Ekvationer

Ekvationstyp 1: Ekvationer av första graden

När vi löser ekvationer av första graden använder vi oss av de fyra grundläggande räknesätten för att beräkna x.

Vid minus tar man plus
Vid plus tar man minus
Vid gånger tar man delat med
Vid delat med tar man gånger

Ekvationstyp 2: Andragradsekvationer
Det finns tre olika typer av andragradsekvationer. För varje typ finns det en lösningsmetod.

Ekvationstyp 3: Allmänna potensekvationer

Vid potensekvationer strävar man efter att få variabelns exponent till 1.

$x^n = C$ ‎‎

$x = C^{1/n}$ ‎

Ekvationstyp 4: Exponentialekvationer

Exponentialekvationer innebär att vi har variabeln som exponent. För att lösa exponentialekvationer måste man använda logaritmer.

$a^x = C$ ‎

$\begin{aligned}x = \frac{\lg C}{\lg a}\end{aligned}$ ‎

Sammanfattning

Ekvationer av första graden − de fyra räknesätten
Andragradsekvationer − roten ur/faktorisera/PQ
Allmänna potensekvationer − höj upp båda sidor
med exponentens inverterade värde
Exponentialekvationer − Logaritmera för att få ner x.

Funktioner

Linjära funktioner

Potensfunktioner

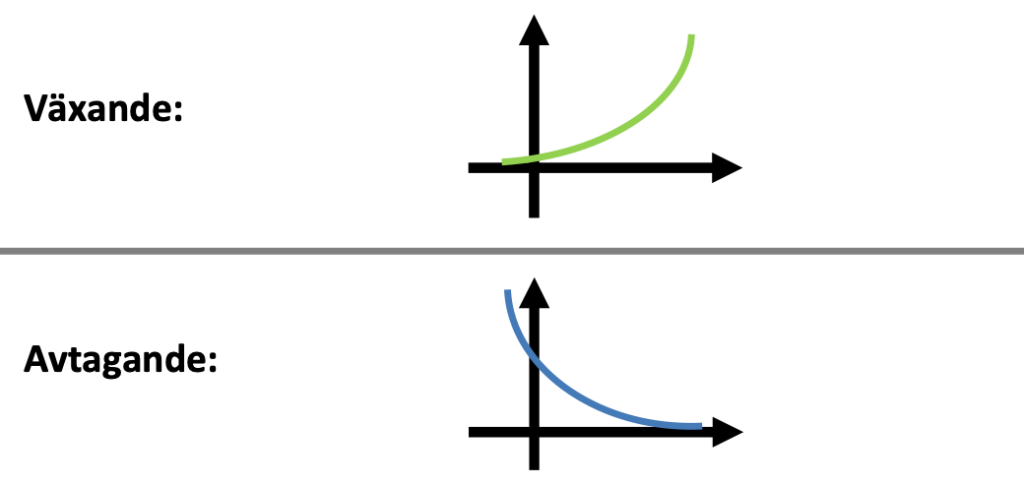
Exponentialfunktioner

Två olika modeller:

$\begin{aligned} &y=C a^{x} \\ &y=C e^{k x} \end{aligned}$ ‎

$y = \text{värde}$ ‎
$C = \text{startvärde}$ ‎
$x = \text{tid}$ ‎
$a / e^k = \text{förändring}$ ‎

Derivata

Sekanter & tangenter

En sekant ger medelförändringen mellan två punkter.
En tangent ger lutningen, derivatan, i en punkt.

Exempel: $f(x)=-0,5 x^{2}+2,5 x+7$
a) Bestäm medellutningen mellan $x=2$ och $x=6$
b) Bestäm lutningen i punkten $x=5$ .

a) För att beräkna medellutningen drar vi en sekant mellan de två punkterna:

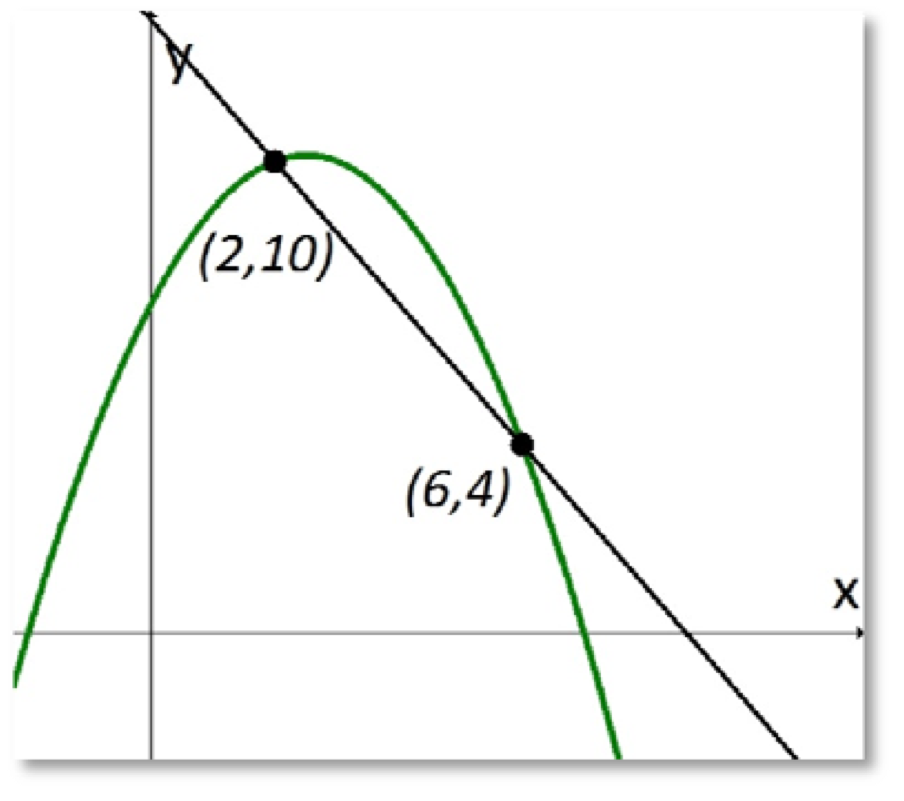
Sekantes lutning beräknas:

$k=\frac{\Delta y}{\Delta x}=\frac{4-10}{6-2}=\frac{-6}{4}=-1,5$ ‎

b) För att beräkna lutningen drar vi en tangent till grafen i punkten $x=5$

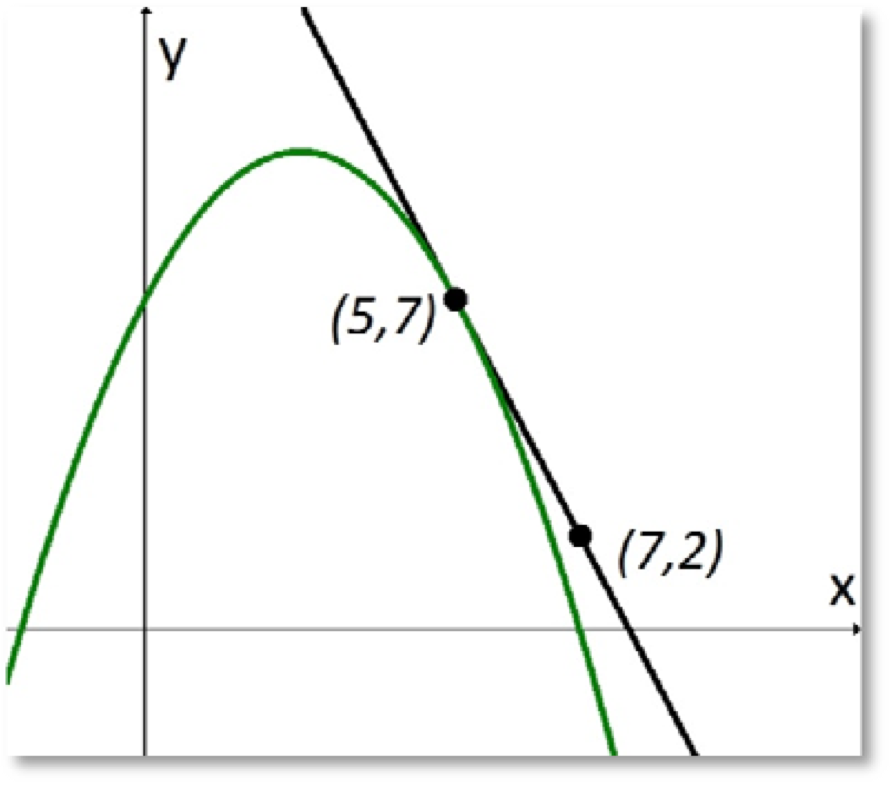
Tangentens lutning beräknas:

$k=\frac{\Delta y}{\Delta x}=\frac{2-7}{7-5}=\frac{-5}{2}=-2,5$ ‎

Svar: a) Medellutningen mellan $x=2$ och $x=6$ är $-1,5$ .‎
b) Lutningen vid $x=5$ är $-2,5$ .

Kom ihåg:

För att ta fram en sekant använder vi två punkter på funktionen.
För att ta fram en tangent drar man en linje som har samma lutning som grafen i just den punkten. Man använder en punkt på funktion och en annan punkt från tangenten.

Derivatans definition

Derivatans definition utgår från en sekant mellan två punkter där avståndet mellan punkterna kallas h.

När man minskar värdet på h blir avståndet mellan punkterna mindre och mindre. Om man gör h oändligt litet hamnar punkterna oändligt nära varandra, och resultat blir att man får fram lutningen i en punkt.

\begin{aligned}f’(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\end{aligned}

Med derivatans definition kan vi ta fram en funktion som beskriver lutningen i varje punkt.

Exempel: Derivera $f({\color{red} x})=2{\color{red} x}^{2}+{\color{red} x}$ med derivatans definition.

\begin{aligned} \frac{f({\color{red} x+h})-f({\color{red} x})}{h}&=\frac{\left(2({\color{red} x+h})^{2}+{\color{red} x+h}\right)-\left(2 {\color{red} x}^{2}+{\color{red} x}\right)}{h}= \\ &=\frac{\left(2 x^{2}+4 x h+2 h^{2}+x+h\right)-\left(2 x^{2}+x\right)}{h}= \\ &=\frac{4 x h+h+2 h^{2}}{h} =\\ &=\frac{h(4 x+1+2 h)}{h} = \\ & =4 x+1+2 h \end{aligned}

Svar: $f’(x)=\lim _{h \rightarrow 0} 4 x+1 + 2h = 4x + 1$

Deriveringsregler

Vi kan ta fram en funktion som beskriver hur grafen förändras med hjälp av deriveringsreglerna.

Regler		Exempel
$f(x)$	$f'(x)$	$f(x)$	$f'(x)$
$x^n$	$n \cdot x^{n-1}$	$2x^3$	$6x^2$
$C \cdot a^x$	$C \cdot \ln a \cdot a^x$	$4 \cdot 1,05^x$	$4 \cdot \ln 1,05 \cdot 1,05^x$
$C \cdot e^{k x}$	$k \cdot C \cdot e^{k x}$	$20 \cdot e^{-0,5 x}$	$-10 \cdot e^{-0,5 x}$
$\ln x$	$\frac{1}{x}$	$10 \ln x$	$\frac{10}{x}$

Extrempunkter

Det finns tre olika typer av extrempunkter. För alla extrempunkter gäller att derivatan är noll.

Teckenschema

När man ska bestämma typ av extrempunkt för en funktion gör man ett teckenschema/teckenstudie

Andraderivata

Andraderivatan beskriver hur derivatan förändras.

Bestämning av extrempunkter

Funktionen $f(x)$ har en extrempunkt där $f^{\prime}(x)=0$ . Med andraderivatan kan bestämma vilken typ av extrempunkt det är:

$f^{\prime \prime}(x)>0 \rightarrow$ minimipunkt
$f^{\prime \prime}(x)<0 \rightarrow$ maximipunkt

Obs! Om $f^{\prime \prime}(x)=0$ måste man göra ett teckenschema för att bestämma typen av extrempunkt.

Exempel: Bestäm extrempunkter till funktionen $f(x)=e^{0,5 x}-2 x$ med hjälp av andraderivata.

Derivera
$f^{\prime}(x)=0,5 e^{0,5 x}-2\\$
$\mathbf{f^{\prime}(x)=0}$
$0,5 e^{0,5 x}-2=0$
$0,5 e^{0,5 x}=2$
$e^{0,5 x}=4$
$0,5 x=\ln 4$
$x=\frac{\ln 4}{0,5} \approx 2,8\\$
Kontrollera typ av extrempunkt med $\mathbf{f^{\prime \prime}(x)}$
$f^{\prime \prime}(x)=0,25 e^{0,5 x}$
$f^{\prime \prime}(2,8)=0,25 e^{0,5 \cdot 2,8} \approx 1>0 \rightarrow$ Buktar upp $\rightarrow$ Minimipunkt $\\$
Ta fram $y$-värde
$f(x)=e^{0,5 x}-2 x$
$f(2,8)=e^{0,5 \cdot 2,8}-2 \cdot 2,8 \approx-1,5$

Svar: Minimipunkt vid $(2,8 ; -1,5)$

Konkavitet

En grafs konkavitet innebär hur den buktar. Förhållandet mellan en grafs konkavitet och andraderivata är:

$f''(x) > 0 \rightarrow$ konkav uppåt
$f''(x) < 0 \rightarrow$ konkav nedåt
$f''(x) = 0 \rightarrow$ byter konkavitet

Förhållandet illustreras i figuren nedan.

Den punkten där grafen byter konkavitet kallas för inflexionspunkt. En inflexionspunkt har kriteriet att andraderivatan är noll men att derivatan inte är noll.

$f''(x) = 0 \text{ och } f'(x) \neq 0 \rightarrow$ inflexionspunkt

Integraler

Primitiva funktioner

En funktion $F(x)$ kallas för en primitiv funktion till $f(x)$ om $F'(x) = f(x)$ .

En primitivfunktion tas fram genom att tillämpa s.k. baklängesderivata.

Regler

$\bm{\underline{f(x)}}$	$\bm{\underline{F(x)}}$
$k$	$kx + C$
$x^n$	$\frac{x^{n+1}}{n+1} + C$
$e^{kx}$	$\frac{e^{kx}}{k} + C$
$a^{x}$	$\frac{a^{x}}{\ln (a)} + C$
$\frac{1}{x}$	$\ln x + C$

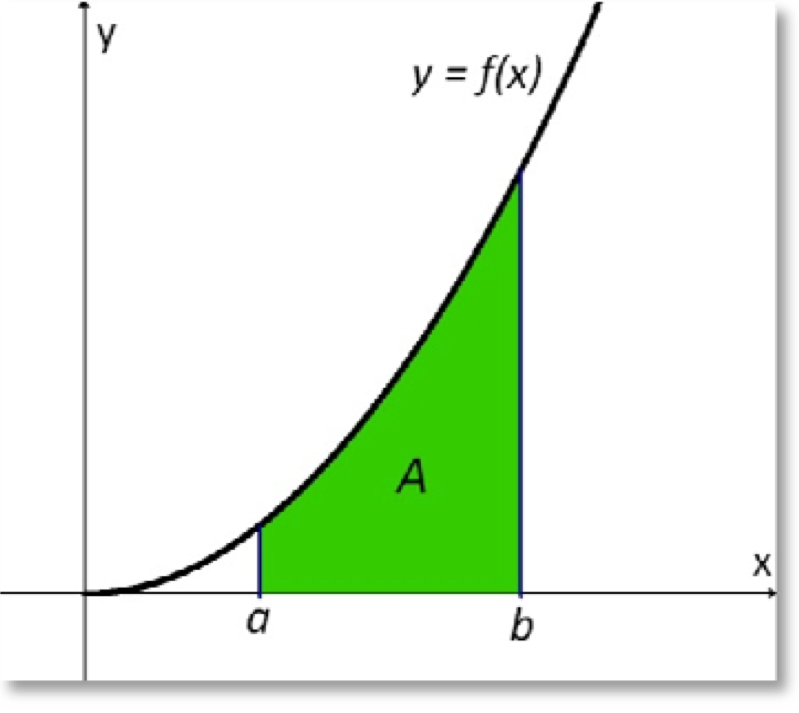
Integraler och areor

En integral innebär summan av funktionsvärden. Integralens värde är samma som arean under grafen så länge grafen är över x‐axeln. När grafen går under x‐axeln uppstår en skillnad mellan integralens värde och arean.

Beräkningar

\begin{aligned}\int_{a}^{b} f(x) d x=[F(x)]_{a}^{b}=F(b)-F(a)\end{aligned}

där $F(x)$ är en primitiv funktion till $f(x)$ .

Trigonometri

Definitioner

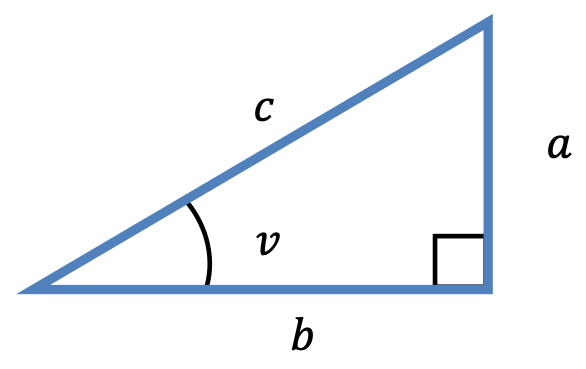
För en rätvinklig triangel gäller följande:

$\sin v = \frac{\text{motstående katet}}{\text{hypotenusan}} = \frac{a}{c}$ ‎

$\cos v = \frac{\text{närliggande katet}}{\text{hypotenusan}} = \frac{b}{c}$ ‎

$\sin v = \frac{\text{motstående katet}}{\text{närliggande katet}} = \frac{a}{b}$ ‎

Enhetscirkeln

I enhetscirkeln kan en punkts koordinater uttryckas med sinus och cosinus.

Triangelsatser

Formler

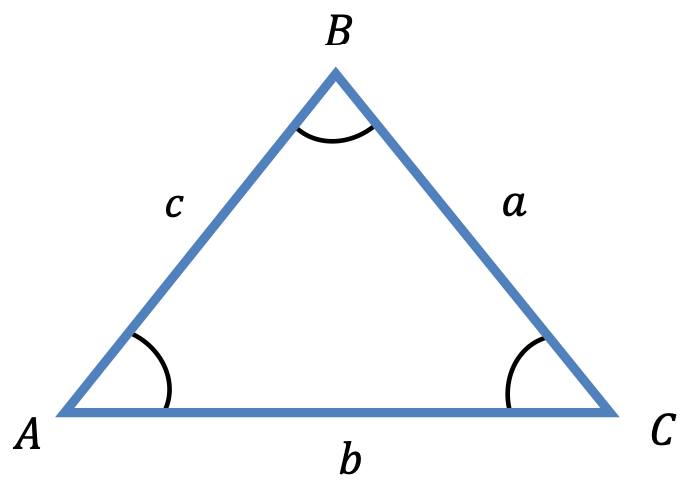
Areasatsen: $T=\frac{b \cdot c \cdot \sin A}{2}$
Sinussatsen: $\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$
Cosinussatsen: $c^{2}=b^{2}+a^{2}-2 b a \cdot \cos C$

Två lösningar

Sinussatsen & Triangelsatsen

När man arbetar med sinus så måste man alltid räkna med att det kan finnas två lösningar, då man kan få två olika vinklar. Detta eftersom $\sin(v) = \sin(180-v)$

Det finns inte två lösningar om:

Vinkelsumman > 180° Alla sidor är kända

Cossinussatsen

När man arbetar med cos finns det ingen möjlighet att man får fram två olika vinklar. Däremot kan det när man använder cossinussatsen bli en andragradsekvation med två rötter. Detta innebär att det i så fall finns två möjliga trianglar.

Exempel: Beräkna vinkel C